Matplotlib是Python的绘图库，它与Numpy一起使用

【引例】
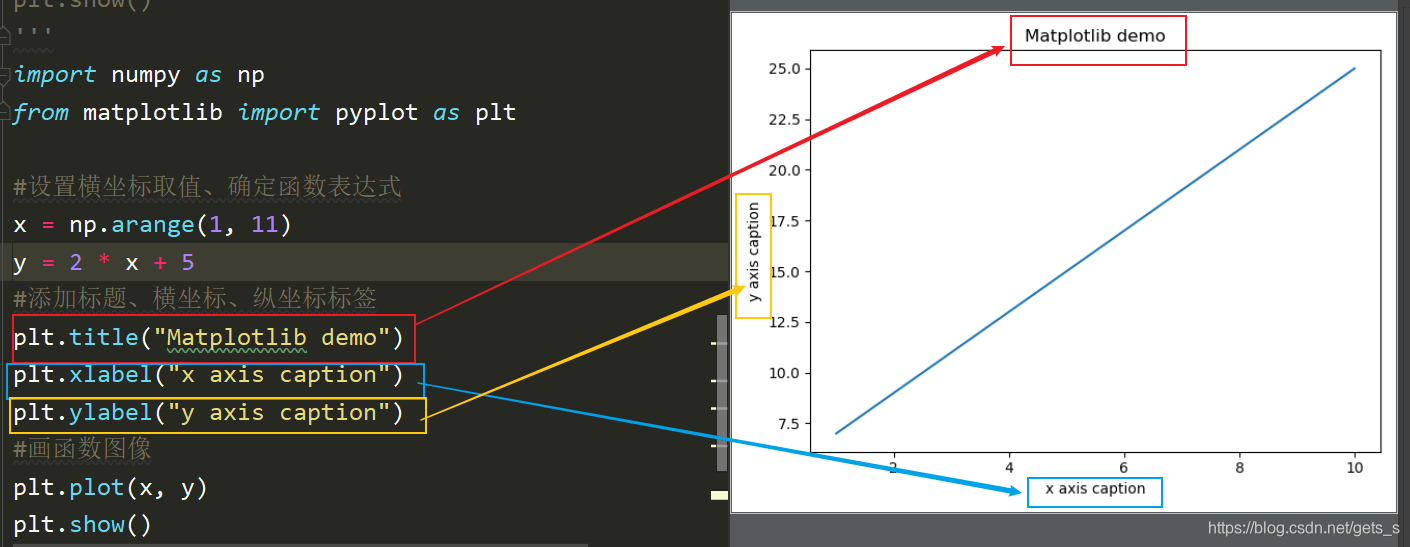
画出y=2*x+5的函数图像

import numpy as np
from matplotlib import pyplot as plt

#设置横坐标取值、确定函数表达式
x = np.arange(1, 11)
y = 2 * x + 5
#添加标题、横坐标、纵坐标标签
plt.title("Matplotlib demo")
plt.xlabel("x axis caption")
plt.ylabel("y axis caption")
#画函数图像
plt.plot(x, y)
plt.show()

【运行结果】

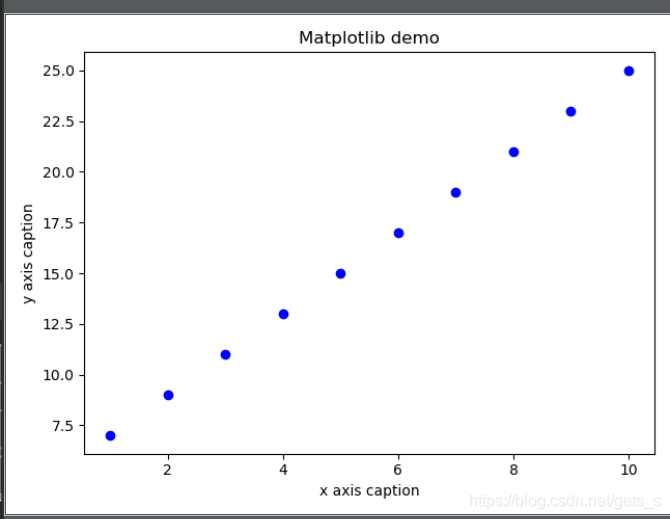
如果需要函数图像以圆点呈现，而不是用线呈现，则需要将

plt.plot(x,y)改为plt.plot(x,y,'ob')

【运行结果】

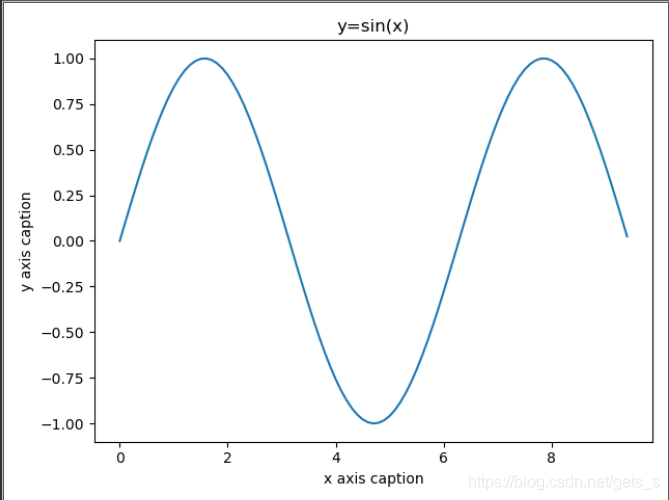
正弦波 y=sin(x)

import numpy as np
from matplotlib import pyplot as plt

#设置横坐标取值、确定函数表达式
x = np.arange(0, 3*np.pi,0.1)
y = np.sin(x)
#添加标题、横坐标、纵坐标标签
plt.title("y=sin(x)")
plt.xlabel("x axis caption")
plt.ylabel("y axis caption")
#画函数图像
plt.plot(x, y)
plt.show()

【运行结果】

余弦函数只需将
y = np.sin(x) 改为 y = np.cos(x)即可

subplot()函数

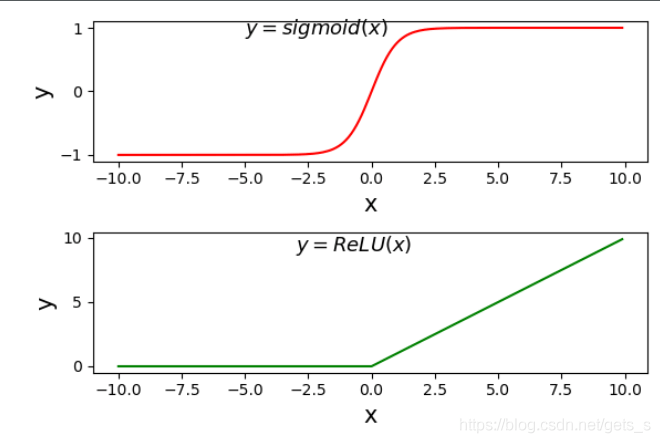
应用subplot（）函数，在同一图中绘制不同的东西

# ReLU和Sigmoid激活函数示意图
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches

#设置图片大小
plt.figure(figsize=(6, 4))

# x是1维数组，数组大小是从-10. 到10.的实数，每隔0.1取一个点
x = np.arange(-10, 10, 0.1)
# 计算 Sigmoid函数
s = (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))


# 计算ReLU函数
y = np.clip(x, a_min = 0., a_max = None)

#########################################################
# 以下部分为画图程序

# 设置两个子图窗口，将Sigmoid的函数图像画在上边
f = plt.subplot(2,1,1)
# 画出函数曲线
plt.plot(x, s, color='r')
# 添加文字说明
plt.text(-5., 0.9, r'$y=sigmoid(x)$', fontsize=13)
# 设置坐标轴格式
currentAxis=plt.gca()
currentAxis.xaxis.set_label_text('x', fontsize=15)
currentAxis.yaxis.set_label_text('y', fontsize=15)

# 将ReLU的函数图像画在下边
f = plt.subplot(2,1,2)
# 画出函数曲线
plt.plot(x, y, color='g')
# 添加文字说明
plt.text(-3.0, 9, r'$y=ReLU(x)$', fontsize=13)
# 设置坐标轴格式
currentAxis=plt.gca()
currentAxis.xaxis.set_label_text('x', fontsize=15)
currentAxis.yaxis.set_label_text('y', fontsize=15)

plt.show()

【运行结果】

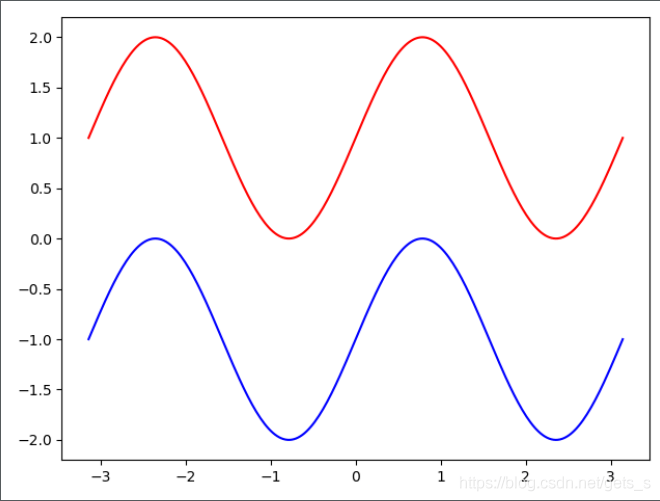
普通图

from matplotlib import pyplot as plt
import numpy as np
n = 256  #n可以理解为曲线的平滑程度
X = np.linspace(-np.pi,np.pi,n,endpoint=True)
Y = np.sin(2*X)

plt.plot(X,Y+1,color='red',alpha=1.00)
plt.plot(X,Y-1,color='blue',alpha=1.00)
plt.show()

【运行结果】

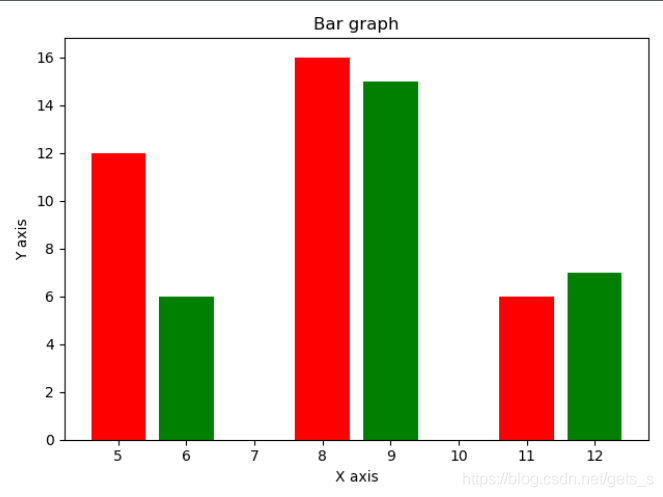
条形图

from matplotlib import pyplot as plt
#数据组1
x =  [5,8,11]  #横坐标
y =  [12,16,6] #对应值
#数据组2
x2 =  [6,9,12] #横坐标
y2 =  [6,15,7] #对应值
plt.bar(x, y, color = 'r', align =  'center')
plt.bar(x2, y2, color =  'g', align =  'center')
plt.title('Bar graph')
plt.ylabel('Y axis')
plt.xlabel('X axis')
plt.show()

【运行结果】

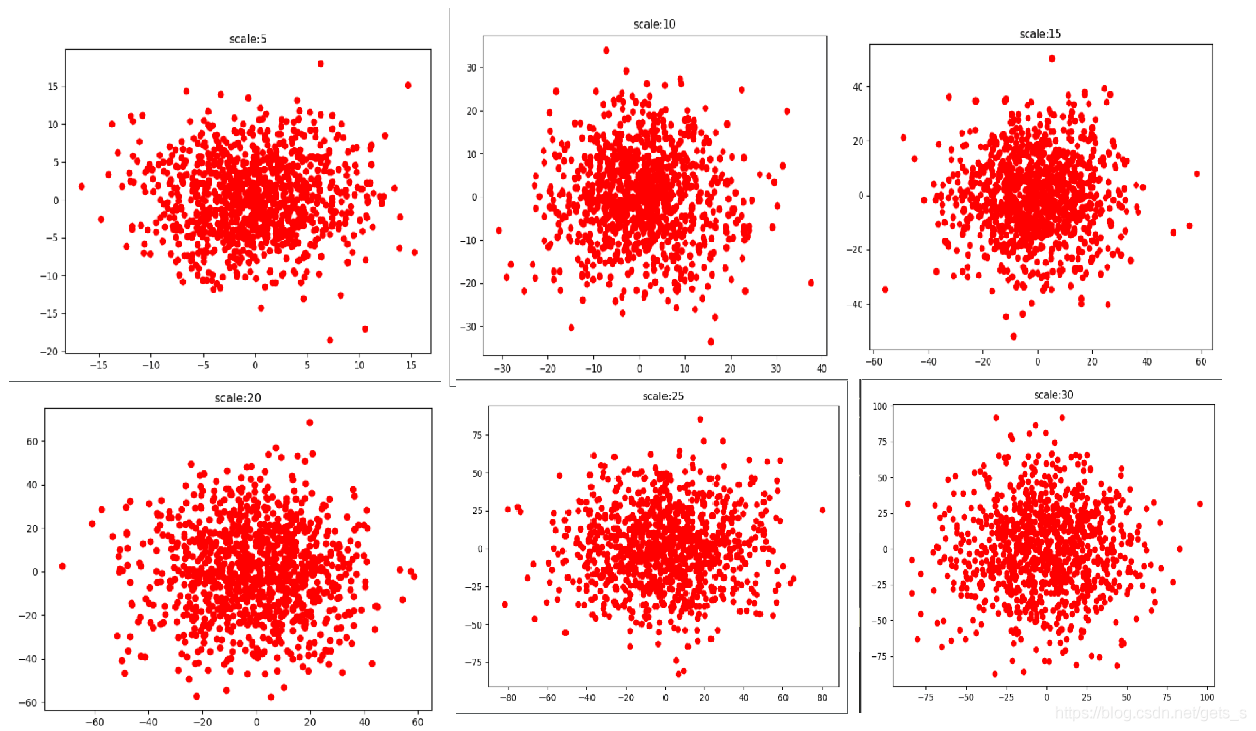
散点图

from matplotlib import pyplot as plt
import numpy as np

n = 1024
X = np.random.normal(0,30,n)
Y = np.random.normal(0,30,n)

plt.title('scale:30')
plt.scatter(X,Y,color='red')
plt.show()

【运行结果】以下分别是方差分别为5，10，15，20，25，30的散点图

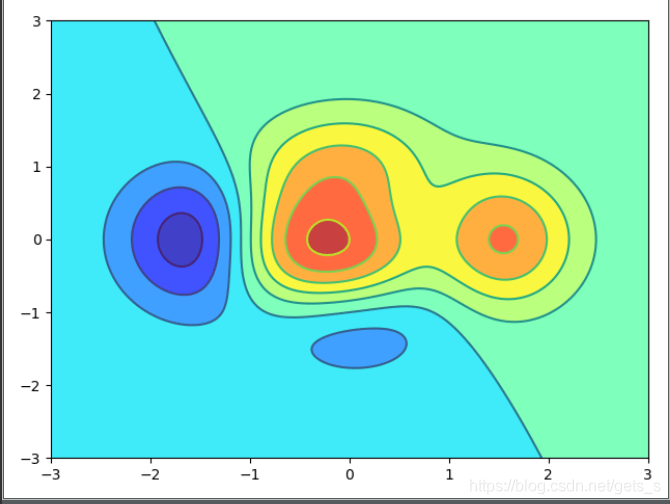
等高线图

from matplotlib import pyplot as plt
import numpy as np

def f(x,y):return(1-x/2+x**5+y**3)*np.exp(-x**2-y**2) #等高线模型

n = 256  #n可以理解为曲线的平滑程度
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)

plt.contourf(X,Y,f(X,Y),8,alpha=.75,cmap='jet')
C = plt.contour(X,Y,f(X,Y),8,color='black',linewidth=.5)
plt.show()

【运行结果】

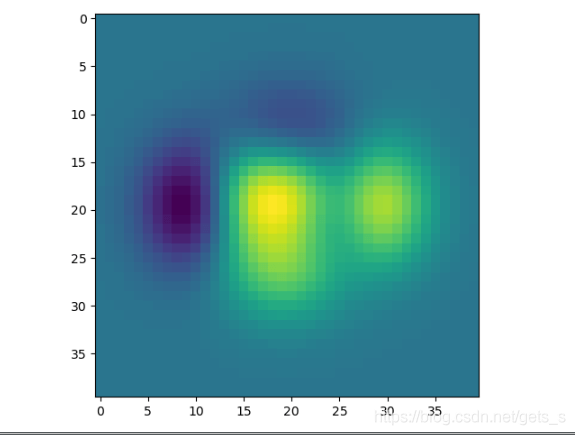
灰度图

from matplotlib import pyplot as plt
import numpy as np

def f(x,y):return(1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 10
x = np.linspace(-3,3,4*n)
y = np.linspace(-3,3,4*n)
X,Y = np.meshgrid(x,y)

plt.imshow(f(X,Y))
plt.show()

【运行结果】

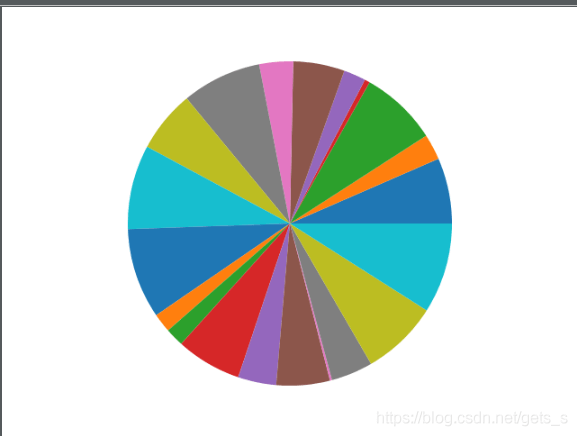
饼状图

from matplotlib import pyplot as plt
import numpy as np

n = 20  #n决定了有多少个分区，该代码显示有20个分区
Z = np.random.uniform(0,1,n)
plt.pie(Z)
plt.show()

【运行结果】

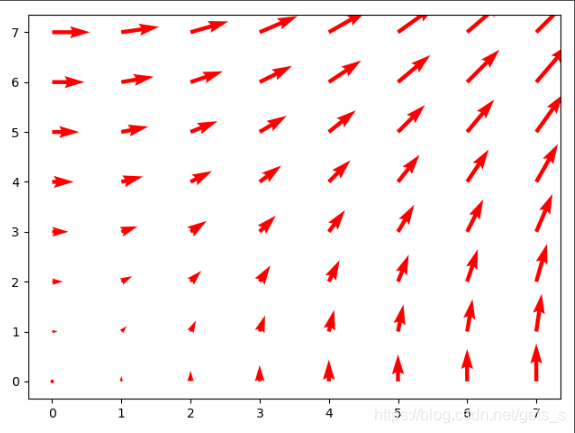
量场图

from matplotlib import pyplot as plt
import numpy as np

n = 8
X,Y = np.mgrid[0:n,0:n]
plt.quiver(X,Y,color="red")
plt.show()

【运行结果】

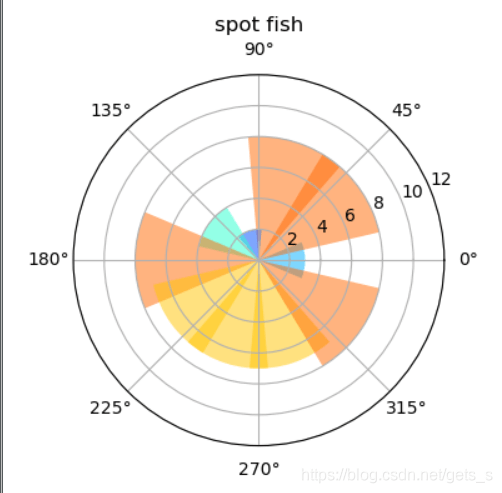
极轴图

from matplotlib import pyplot as plt
import numpy as np

plt.figure(figsize=(4,4))
ax1 = plt.subplot(111,projection='polar')
ax1.set_title('spot fish')
ax1.set_rlim(0,12)

data = np.random.randint(1,10,10)
theta = np.arange(0,2*np.pi,2*np.pi/10)

bar = ax1.bar(theta,data,alpha=0.5)
for r,bar in zip(data,bar):
    bar.set_facecolor(plt.cm.jet(r/10.))
plt.show()

【运行结果】

3D图

到此这篇关于使用 NumPy 和 Matplotlib 绘制函数图的文章就介绍到这了,更多相关NumPy Matplotlib 内容请搜索hwidc以前的文章或继续浏览下面的相关文章希望大家以后多多支持hwidc！

【本文由：专业的印度服务器 提供,感谢支持】