c++基础算法动态DP解决CoinChange问题
目录
- 问题来源
- 问题简述
- 解决方案
- 真正的DP
- 补充——硬币不能重复使用
- 补充2——不同顺序表示不同组合
- 结束语
问题来源
这是Hackerrank上的一个比较有意思的问题,详见下面的链接:
https://www.hackerrank.com/challenges/ctci-coin-change
问题简述
给定m个不同面额的硬币,C={c0, c1, c2…cm-1},找到共有几种不同的组合可以使得数额为n的钱换成等额的硬币(每种硬币可以重复使用)。
比如:给定m=3,C={2,1,3},n=4,那么共有4种不同的组合可以换算硬币
{1,1,1,1}
{1,1,2}
{2,2}
{1,3}
解决方案
基本思路是从硬币(coins)的角度出发,考虑coins[0]仅使用1次的情况下有几种组合,coins[0]仅使用2次的情况下有几种组合,依次类推,直到 (n - coins[0] * 使用次数) < 0 则终止,而每个 (n - coins[0]) 下又可以递归 (n - coins[0] - coins[1]) 的情况,直到考虑完所有的硬币。
这样说可能还是没有说清楚,下面以m=3,C={1,2,3},n=4为例,用图来说明一下(建议结合程序一起看)。
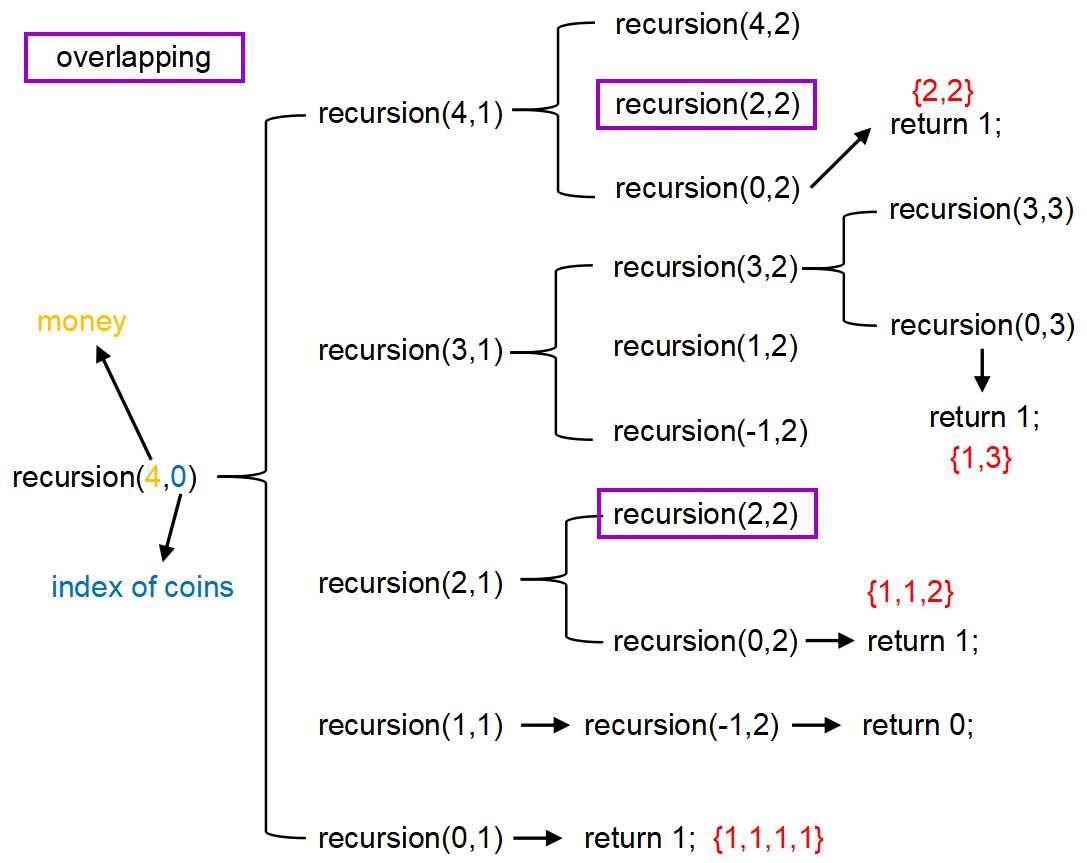
图1:coin Change不完整递归图
上图没有画出完整的递归过程(有点麻烦~偷了个懒),不过把能得出结果的几条路径都描绘出来了。其中,recursion(money, index)中,money指的是还没有进行兑换的钱,index指的是要用哪个coin去兑换,比如这里的0指的是coins[0]=1,1指的是coins[1]=2,2指的是coins[2]=3,3是不存在的,这也是程序的终止条件之一。 注意到再递归的过程中有重叠子问题(我用紫色标注出了其中一个),这就可以用动态规划的思想来解决了,创建一块空间来存储已经算过的结果就可以了。 # 程序代码 好了,下面直接上程序了,结合图看好理解~
#include <iostream>
#include <unordered_map>
#include <string>
#include <vector>
using namespace std;
long long recursion(vector<int> &coins, int money, int index, unordered_map<string, int> &memo){
//终止条件2个
if (0 == money)
return 1;
if (index >= coins.size() || money < 0)
return 0;
string key = to_string(money) + " , " + to_string(index);
//如果记录中有的话就直接返回就好了
if (memo.find(key) != memo.end())
return memo[key];
long long res = 0;
int remaining = money;
while(remaining >= 0){
res += recursion(coins, remaining, index + 1, memo);
remaining -= coins[index];
}
//记录一下
memo[key] = res;
return res;
}
long long make_change(vector<int> coins, int money) {
//用哈希表来记录 <剩下的钱-用的硬币>:换硬币的组合数
unordered_map<string, int> memo;
long long res = recursion(coins, money, 0, memo);
return res;
}
int main(){
int n;
int m;
cin >> n >> m;
vector<int> coins(m);
for(int coins_i = 0;coins_i < m;coins_i++){
cin >> coins[coins_i];
}
cout << make_change(coins, n) << endl;
return 0;
}
Sample Input
10 4
2 5 3 6
Sample Output
5
真正的DP
上面的那段代码是以自顶向下的方式来解决问题的,思路比较清晰,而真正的动态规划是自底向上的,思路其实也差不多,下面给出代码~
long long make_change(vector<int> coins, int money) {
vector<long long> memo(money + 1, 0);
memo[0] = 1;
for (int i = 0; i < coins.size(); i++){
for (int j = coins[i]; j <= money; j++){
memo[j] += memo[j - coins[i]];
}
}
return memo[money];
}
补充——硬币不能重复使用
如果每种硬币不能重复使用的话,又该怎么办呢?这只需要再程序上做一些小的改动就可以了,真的是非常神奇~
要细细体会一下~
long long make_change(vector<int> coins, int money) {
vector<long long> memo(money + 1, 0);
memo[0] = 1;
for (int i = 0; i < coins.size(); i++){
//改动处:由从前往后改成了从后往前,略去了重复的情况
for (int j = money; j >= coins[i]; j--){
memo[j] += memo[j - coins[i]];
}
}
return memo[money];
}
补充2——不同顺序表示不同组合
然后再来变一变,如果每种硬币可以使用无限多次,但是不同的顺序表示不同的组合,那么又有多少种组合呢?
比如:
coins = [1, 2, 3]
money = 4可能的组合情况有:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)注意,不同的顺序序列表示不同的组合~
所以结果是7。
这种情况下的代码是:
long long make_change(vector<int> coins, int money) {
vector<long long> memo(money + 1, 0);
memo[0] = 1;
//改变了里外循环的顺序
for (int i = 1; i <=money; i++){
for (int j = 0; j < coins.size(); j++){
if (i - coins[j] >= 0)
memo[i] += memo[i - coins[j]];
}
}
return memo[money];
}
要仔细体会一下三种情况下的区别和代码微妙的变化~
结束语
动态规划的代码量其实不大,但是思维量还是挺大的,要写正确还是要折腾挺久的~
本人是初学者,如有错误,还请指正~希望大家以后多多支持海外IDC网!
