一文学会数据结构-堆

编辑: admin 分类: c#语言 发布时间: 2021-12-12 来源:互联网
目录
  • 1.堆
  • 2.堆的实现
    • 2.1堆的向下调整算法(建小堆)
    • 2.2 堆向下调整算法(建小堆)实现
    • 2.3 堆的向上调整算法
    • 2.4 向上调整算法(建小堆)实现
    • 2.5 数组建堆算法(建小堆)
    • 2.6 数组建堆算法(建小堆)实现
    • 2.7 堆排序(降序)
    • 2.8 堆排序(降序)实现
    • 2.9 建堆的时间复杂度

1.堆

大根堆：所有父节点大于等于孩子节点

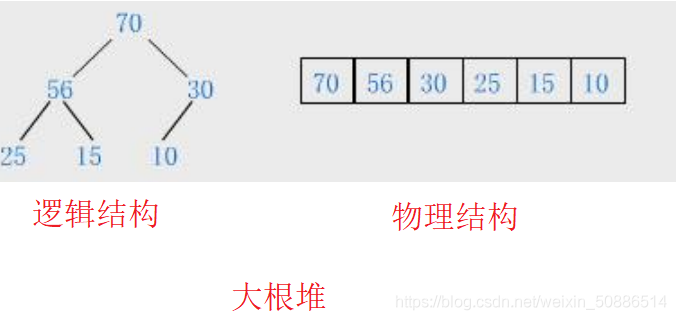
在这里插入图片描述

小根堆：所有父节点小于等于孩子节点

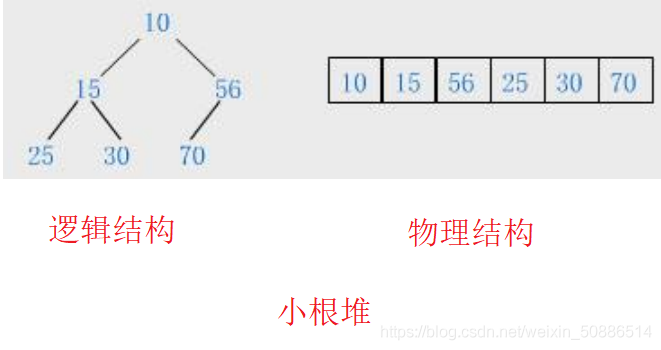
在这里插入图片描述

堆的性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值

• 堆总是一棵完全二叉树

2.堆的实现

堆的实现请点击—> 实现堆排序实例

现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。

int a[] = {27,15,19,18,28,34,65,49,25,37};

2.1堆的向下调整算法(建小堆)

向下调整算法-前提：当前树的左右子树必须都是一个小堆
向下调整算法的核心思想：选出左右孩子中小的哪一个，跟父亲交换，小的往上浮，大的往下沉，如果要建大堆则相反

如下图所示为一个向下调整法调小堆

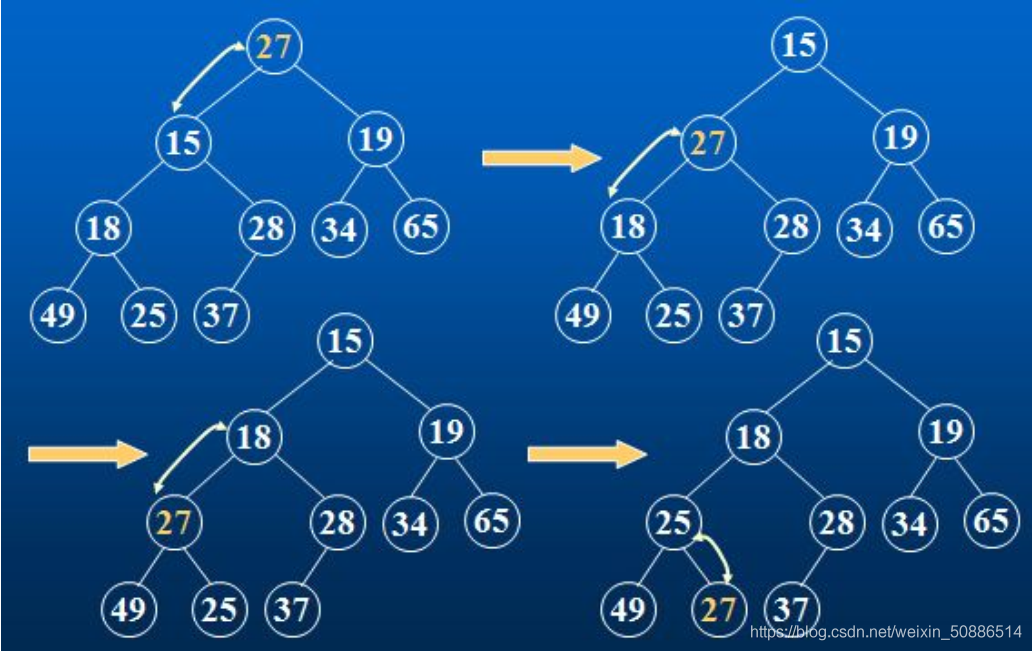
在这里插入图片描述

2.2 堆向下调整算法(建小堆)实现

//堆向下调整算法
//建小堆
void AdjustDown(int* a, int n, int root)
{
	int parent = root;
	int child = parent * 2 + 1;
	//孩子超过数组下标结束
	while (child < n)
	{
		//child始终左右孩子中小的那个
		if (a[child + 1] < a[child] && child + 1 <n)//防止没有右孩子
		{
			++child;
		}
		//小的往上浮，大的往下浮
		if (a[child] < a[parent])
		{
			int tem = a[parent];
			a[parent] = a[child];
			a[child] = tem;
			parent = child;
			child = parent * 2 + 1;
		}
		//中途child>parent则已满足小堆，直接break
		else
		{
			break;
		}
	}
}

2.3 堆的向上调整算法

使用场景：向堆中插入数据，需要使用向上调整算法调整，因为向堆中插入数据是将数据插入到下标为size的位置，此时就不满足小堆(大堆)，因此，需要堆其进行调整，向上调整算法和向下调整算法思路类似，此处以小堆为例，向上调整法只需从插入的节点位置开始和父节点比较，若a[chaild]<a[parent],则交换，若a[chaild]>=a[parent]则说明越界满足小堆，直接break

如下图所示插入一个数据使用向上调整法调整

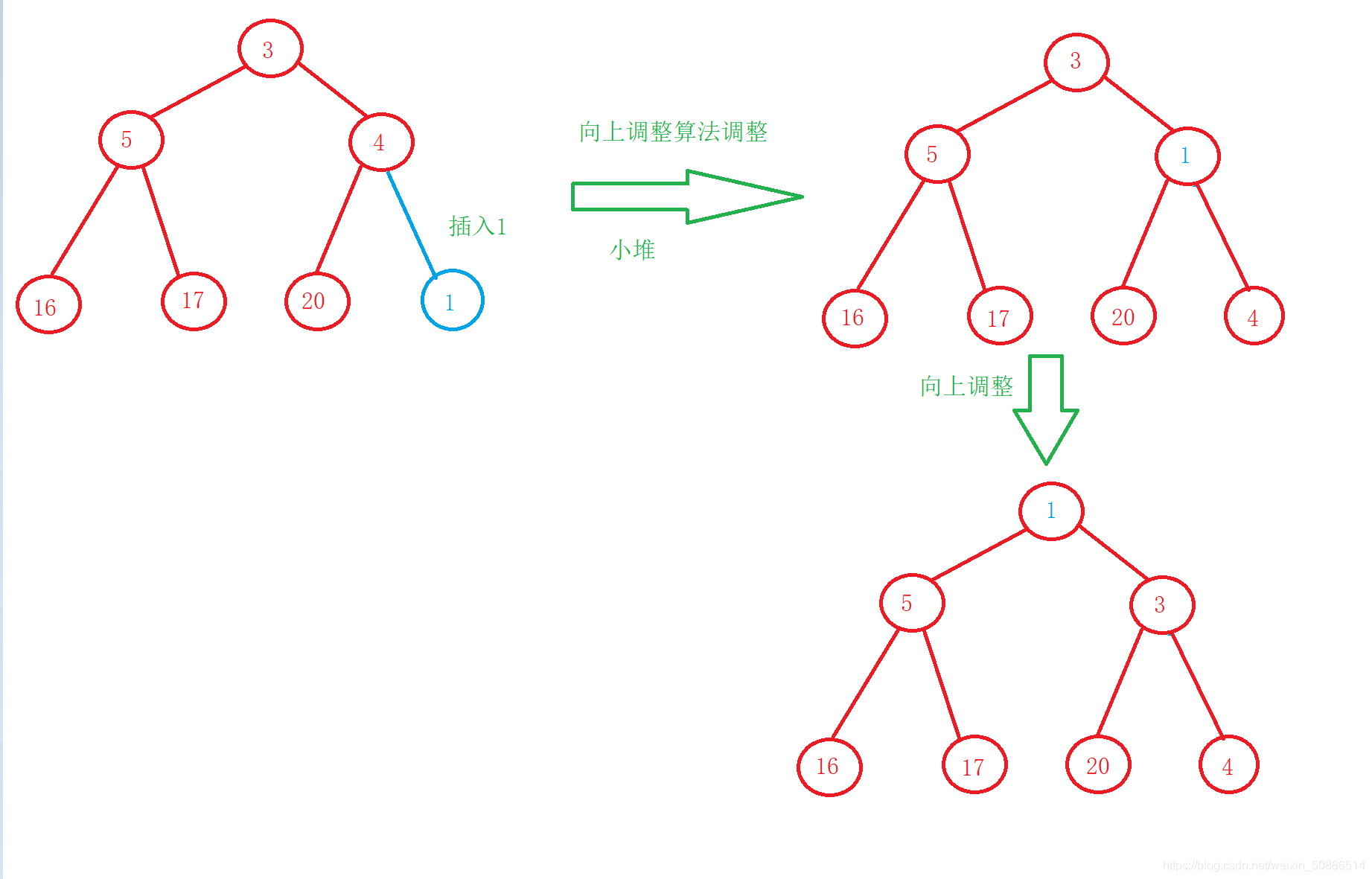
在这里插入图片描述

2.4 向上调整算法(建小堆)实现

//堆的向上调整算法
//建小堆
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			int tem = a[parent];
			a[parent] = a[child];
			a[child] = tem;
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

2.5 数组建堆算法(建小堆)

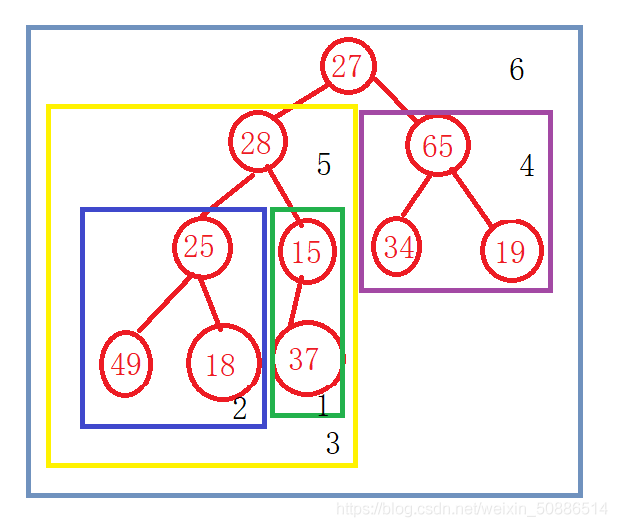
若左右子树不是小堆——想办法把左右子树处理成小堆
可以从倒数第一个非叶子节点的位置开始向下调整

如下图所示可以按图中的步骤依次向下调整
最后一个非叶子节点的下标为 (n-1-1)/2

在这里插入图片描述

2.6 数组建堆算法(建小堆)实现

	int n = sizeof(a) / sizeof(int);
	//数组建堆算法
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(arr, n, i);
	}

2.7 堆排序(降序)

下面我们将上面建好的小堆进行降序排序

堆排序(降序)的核心思想：因为建小堆可以选出最小的数即根节点，我们将每次建好的小堆的最后一个叶子节点和根节点进行交换，交换后不把最后一个数看作堆里的数据，此时根的左右子树依旧是大堆，然后我们再用向下调整算法选出次小的如此循环直到堆里剩一个数结束

• 升序建大堆
• 降序建小堆

2.8 堆排序(降序)实现

//降序
void HeapSort(int* a, int n)
{
	//建小堆
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	//把最小的换到最后一个位置，不把最后一个数看作堆里的
	//每次选出剩下数中最小的
	//从后往前放
	while (end > 0)
	{
		int tem = a[end];
		a[end] = a[0];
		a[0] = tem;
		//选出次小的数
		AdjustDown(a, end, 0);
		--end;
	}
}

2.9 建堆的时间复杂度

最坏的情况及满二叉树，且每个节点都需要调整

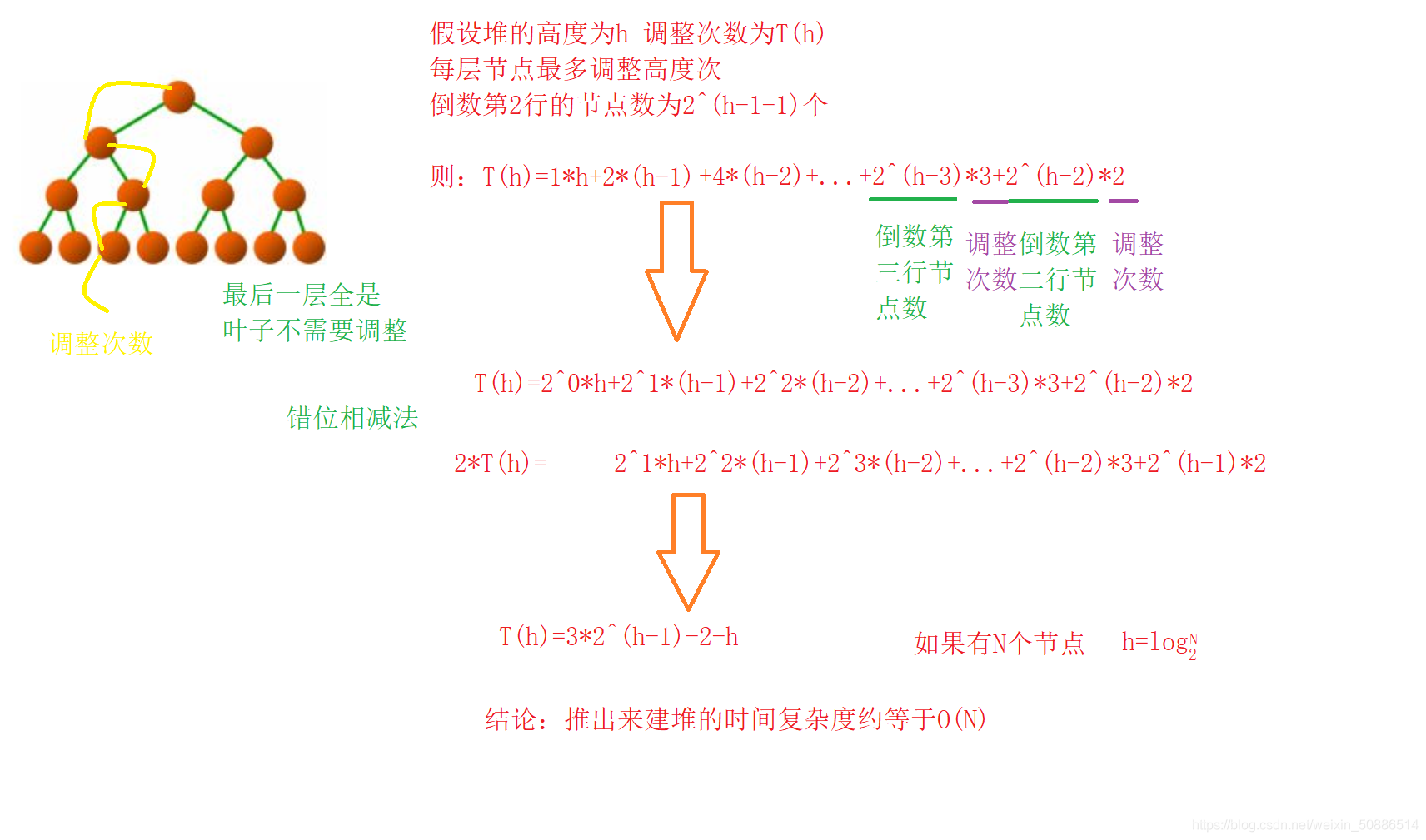
在这里插入图片描述

由以上推论过程可得建堆的时间复杂度为O(N);
向下调整算法的时间复杂度为O(log2N);
所以堆排序的时间复杂度为O(N*log2N);

到此这篇关于一文学会数据结构-堆的文章就介绍到这了,更多相关堆内容请搜索海外IDC网以前的文章或继续浏览下面的相关文章希望大家以后多多支持海外IDC网！

【文章出处:欧洲服务器】
更多阅读