python进阶TensorFlow神经网络拟合线性及非线性函数
目录
- 一、拟合线性函数
- 生成随机坐标
- 神经网络拟合
- 代码
- 二、拟合非线性函数
- 生成二次随机点
- 神经网络拟合
- 代码
一、拟合线性函数
学习率0.03,训练1000次:
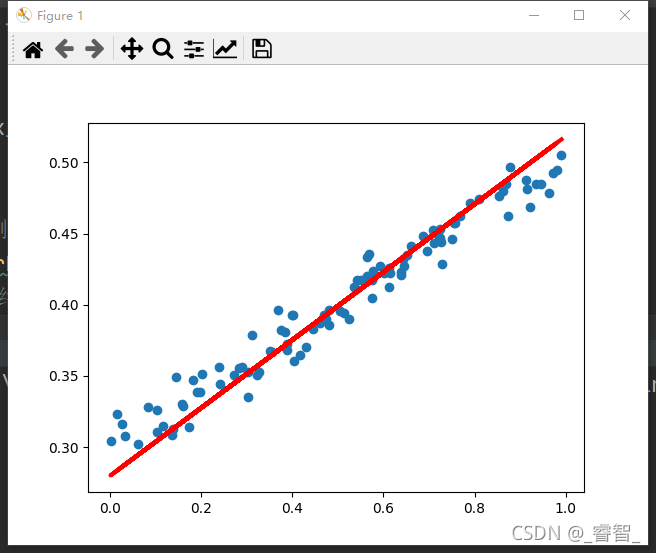
学习率0.05,训练1000次:
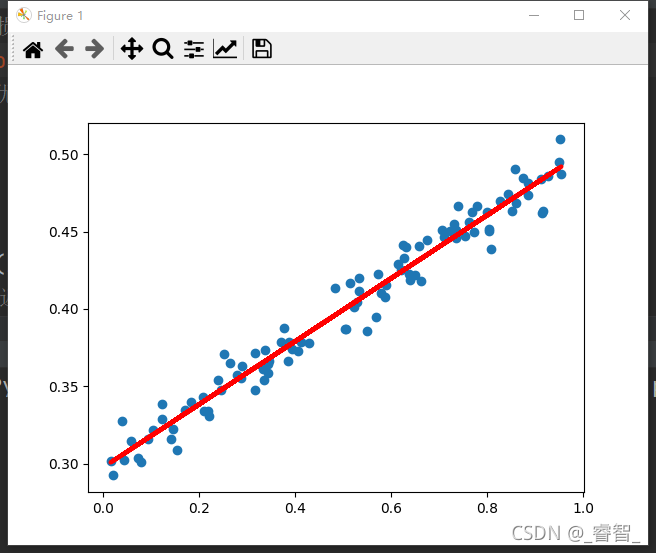
学习率0.1,训练1000次:
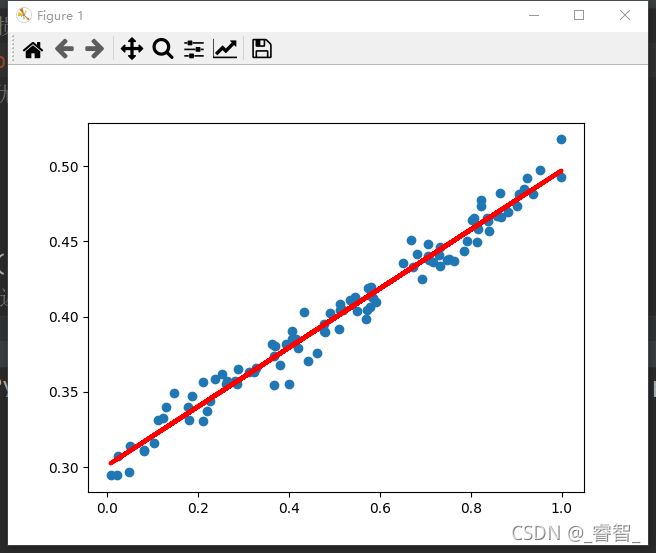
可以发现,学习率为0.05时的训练效果是最好的。
生成随机坐标
1、生成x坐标
2、生成随机干扰
3、计算得到y坐标
4、画点
# 生成随机点
def Produce_Random_Data():
global x_data, y_data
# 生成x坐标
x_data = np.random.rand(100)
# 生成随机干扰
noise = np.random.normal(0, 0.01, x_data.shape)
# 均值 标准差 输出的形状
# 计算y坐标
y_data = 0.2 * x_data + 0.3 + noise
# 画点
plt.scatter(x_data, y_data)
神经网络拟合
1、创建神经网络
2、设置优化器与损失函数
3、训练(根据已有数据)
4、预测(给定横坐标,预测纵坐标)
# 创建神经网络(训练及预测)
def Neural_Network():
# 1 创建神经网络
model = tf.keras.Sequential()
# 为神经网络添加层
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
# 隐藏层 神经元个数 输入神经元个数
# 2 设置优化器与损失函数
model.compile(optimizer=SGD(0.05), loss='mse')
# 优化器 学习率0.05 损失函数
# SGD:随机梯度下降法
# mse:均方误差
# 3 训练
for i in range(1000):
# 训练数据并返回损失
loss = model.train_on_batch(x_data, y_data)
# print(loss)
# 4 预测
y_pred = model.predict(x_data)
# 5 显示预测结果(拟合线)
plt.plot(x_data, y_pred, 'r-', lw=3) #lw:线条粗细
代码
# 拟合线性函数
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.optimizers import SGD
# 生成随机点
def Produce_Random_Data():
global x_data, y_data
# 生成x坐标
x_data = np.random.rand(100)
# 生成随机干扰
noise = np.random.normal(0, 0.01, x_data.shape)
# 均值 标准差 输出的形状
# 计算y坐标
y_data = 0.2 * x_data + 0.3 + noise
# 画点
plt.scatter(x_data, y_data)
# 创建神经网络(训练及预测)
def Neural_Network():
# 1 创建神经网络
model = tf.keras.Sequential()
# 为神经网络添加层
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
# 隐藏层 神经元个数 输入神经元个数
# 2 设置优化器与损失函数
model.compile(optimizer=SGD(0.05), loss='mse')
# 优化器 学习率0.05 损失函数
# SGD:随机梯度下降法
# mse:均方误差
# 3 训练
for i in range(1000):
# 训练数据并返回损失
loss = model.train_on_batch(x_data, y_data)
# print(loss)
# 4 预测
y_pred = model.predict(x_data)
# 5 显示预测结果(拟合线)
plt.plot(x_data, y_pred, 'r-', lw=3) #lw:线条粗细
# 1、生成随机点
Produce_Random_Data()
# 2、神经网络训练与预测
Neural_Network()
plt.show()
二、拟合非线性函数
第一层10个神经元:
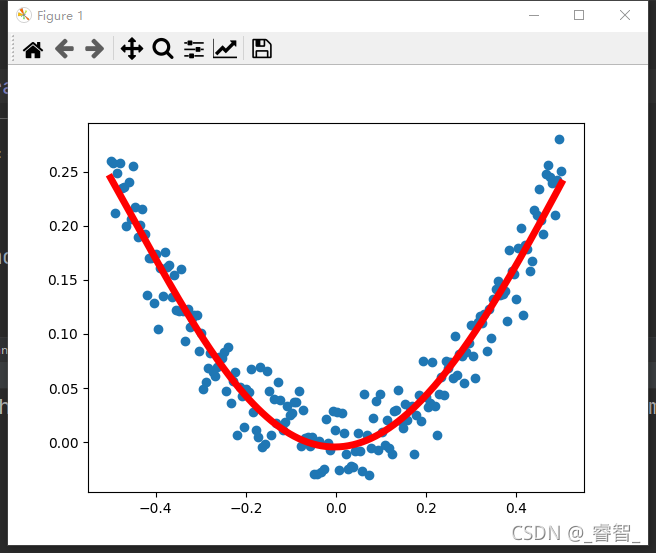
第一层5个神经元:
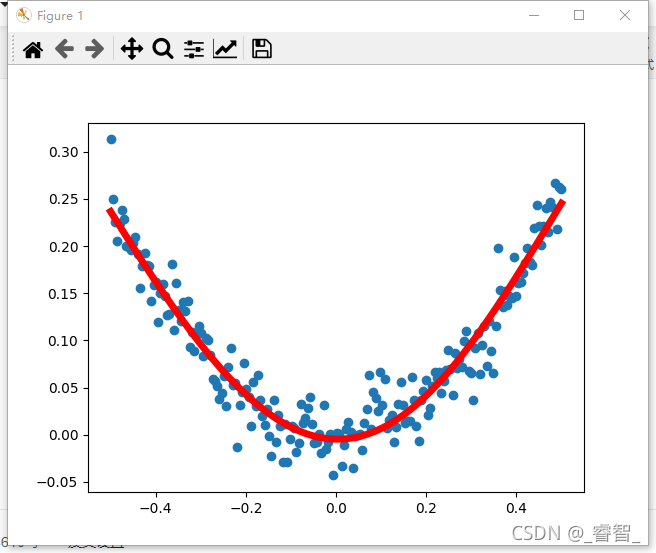
我感觉第一层5个神经元反而训练效果比10个的好。。。
生成二次随机点
步骤:
1、生成x坐标
2、生成随机干扰
3、计算y坐标
4、画散点图
# 生成随机点
def Produce_Random_Data():
global x_data, y_data
# 生成x坐标
x_data = np.linspace(-0.5, 0.5, 200)[:, np.newaxis]
# 增加一个维度
# 生成噪声
noise = np.random.normal(0, 0.02, x_data.shape)
# 均值 方差
# 计算y坐标
y_data = np.square(x_data) + noise
# 画散点图
plt.scatter(x_data, y_data)
神经网络拟合
步骤:
1、创建神经网络
2、设置优化器及损失函数
3、训练(根据已有数据)
4、预测(给定横坐标,预测纵坐标)
5、画图
# 神经网络拟合(训练及预测)
def Neural_Network():
# 1 创建神经网络
model = tf.keras.Sequential()
# 添加层
# 注:input_dim(输入神经元个数)只需要在输入层重视设置,后面的网络可以自动推断出该层的对应输入
model.add(tf.keras.layers.Dense(units=5, input_dim=1, activation='tanh'))
# 神经元个数 输入神经元个数 激活函数
model.add(tf.keras.layers.Dense(units=1, activation='tanh'))
# 2 设置优化器和损失函数
model.compile(optimizer=SGD(0.3), loss='mse')
# 优化器 学习率 损失函数(均方误差)
# 3 训练
for i in range(3000):
# 训练一次数据,返回loss
loss = model.train_on_batch(x_data, y_data)
# 4 预测
y_pred = model.predict(x_data)
# 5 画图
plt.plot(x_data, y_pred, 'r-', lw=5)
代码
# 拟合非线性函数
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.optimizers import SGD
# 生成随机点
def Produce_Random_Data():
global x_data, y_data
# 生成x坐标
x_data = np.linspace(-0.5, 0.5, 200)[:, np.newaxis]
# 增加一个维度
# 生成噪声
noise = np.random.normal(0, 0.02, x_data.shape)
# 均值 方差
# 计算y坐标
y_data = np.square(x_data) + noise
# 画散点图
plt.scatter(x_data, y_data)
# 神经网络拟合(训练及预测)
def Neural_Network():
# 1 创建神经网络
model = tf.keras.Sequential()
# 添加层
# 注:input_dim(输入神经元个数)只需要在输入层重视设置,后面的网络可以自动推断出该层的对应输入
model.add(tf.keras.layers.Dense(units=5, input_dim=1, activation='tanh'))
# 神经元个数 输入神经元个数 激活函数
model.add(tf.keras.layers.Dense(units=1, activation='tanh'))
# 输出神经元个数
# 2 设置优化器和损失函数
model.compile(optimizer=SGD(0.3), loss='mse')
# 优化器 学习率 损失函数(均方误差)
# 3 训练
for i in range(3000):
# 训练一次数据,返回loss
loss = model.train_on_batch(x_data, y_data)
# 4 预测
y_pred = model.predict(x_data)
# 5 画图
plt.plot(x_data, y_pred, 'r-', lw=5)
# 1、生成随机点
Produce_Random_Data()
# 2、神经网络训练与预测
Neural_Network()
plt.show()
以上就是python进阶TensorFlow神经网络拟合线性及非线性函数的详细内容,更多关于TensorFlow神经网络拟合线性及非线性函数的资料请关注hwidc其它相关文章!
