Python一些基本的图像操作和处理总结

编辑: admin 分类: python 发布时间: 2021-12-23 来源:互联网

一、Python图像处理PIL库

1.1 转换图像格式

# PIL（Python Imaging Library）
from PIL import Image
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取的是图像，cv.imread读取的是array，Image.open()显示的图像是RGB
pil_im=Image.open('pic/kobe_mamba.jpg')

subplot(121),plt.title('原图'),axis('off')
imshow(pil_im)

pil_im_gray=pil_im.convert('L')
subplot(122),plt.title('灰度图'),xticks(x,()),yticks(y,())
imshow(pil_im_gray)

在这里插入图片描述

# 转换图像格式 PIL中有九种不同模式。分别为1，L，P，RGB，RGBA，CMYK，YCbCr，I，F。
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
plt.rcParams['font.sans-serif'] = ['SimHei']

pil_im=Image.open('pic/apple.jpg')

# 模式1 二值图像

pil_im_binary=pil_im.convert('1')
subplot(231),plt.title('二值图像'),axis('off'),imshow(pil_im_binary)

pil_im_binary.getpixel((10,10))

# 模式2 L = R * 299/1000 + G * 587/1000+ B * 114/1000 灰度模式 0表示黑，255表示白

# 模式3 P模式为8位彩色图像,通过RGB调色

pil_im_p=pil_im.convert('P')

subplot(232),plt.title('调色P图像'),axis('off'),imshow(pil_im_p)

# 模式4 模式“RGBA”为32位彩色图像，它的每个像素用32个bit表示，其中24bit表示红色、绿色和蓝色三个通道，另外8bit（255）表示alpha通道，255表示不透明。

pil_im_RGBA=pil_im.convert('RGBA')

subplot(233),plt.title('RGBA图像'),axis('off'),imshow(pil_im_RGBA)

# 模式5 CMYK 三原色+黑色，每个像素由32位表示
# C = 255 - R, M = 255 - G, Y = 255 - B, K = 0

pil_im_CMYK=pil_im.convert('CMYK')

subplot(234),plt.title('CMYK图像'),axis('off'),imshow(pil_im_CMYK)

#模式6 YCbcr 24位bit表示 Y= 0.257*R+0.504*G+0.098*B+16 Cb = -0.148*R-0.291*G+0.439*B+128 Cr = 0.439*R-0.368*G-0.071*B+128

pil_im_YCbCr=pil_im.convert('YCbCr')

subplot(235),plt.title('YCbCr图像'),axis('off'),imshow(pil_im_YCbCr)

# 模式7 I模式略 与L模式显示相同 ，只不过是32bit

# 模式8 F模式略 像素保留小数，其余与L模式相同

在这里插入图片描述

1.2 缩略图

# PIL（Python Imaging Library）
from PIL import Image
from pylab import *
plt.rcParams['font.sans-serif'] = ['SimHei']

pil_im=Image.open('pic/kobe_mamba.jpg')


# 创建缩略图 且可以指定大小

pil_im.thumbnail((120,120))

plt.title('缩略图'),xticks(x,()),yticks([])
imshow(pil_im)

在这里插入图片描述

1.3 复制、粘贴和旋转、调整尺寸

# 元组坐标分别为（左、上、右、下），从而标出了一块区域，相当于[100:400,100:400]

box=(100,100,400,400)

region=pil_im.crop(box)
# 旋转180度
region=region.transpose(Image.ROTATE_180)

figure(figsize=(5,5))

plt.title('复制区域'),axis('off')


imshow(region)
#粘贴


pil_im=Image.open('pic/kobe_mamba.jpg')

pil_im.paste(region,box)

figure(figsize=(5,5))

plt.title('粘贴后的图像'),axis('off')

imshow(pil_im)

# 调整尺寸和旋转 resize 和 rotate 函数

out=pil_im.resize((128,128))

out=pil_im.rotate(45)

在这里插入图片描述

第二张图是box旋转了180度再粘贴的结果

二、Matoplotlib库基础学习

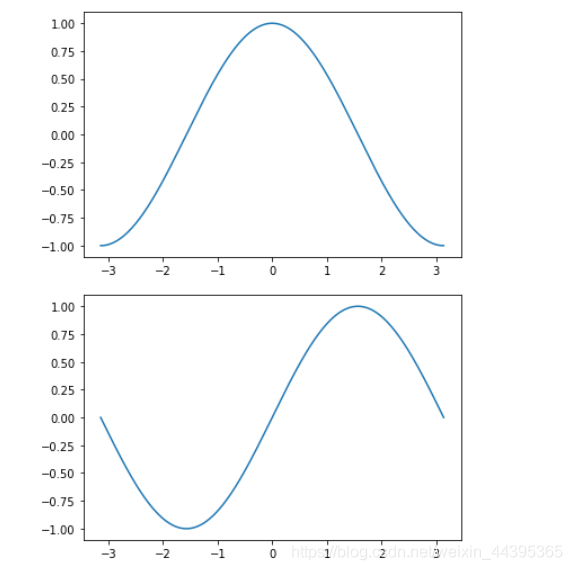
# 基本绘图
import numpy as np
import matplotlib.pyplot as plt
from numpy import pi
from pylab import *

x=np.linspace(-pi,pi,256)
y,z=np.cos(x),np.sin(x)
figure()
plt.plot(x,y)
figure()
plt.plot(x,z)
plt.show()

两张绘图

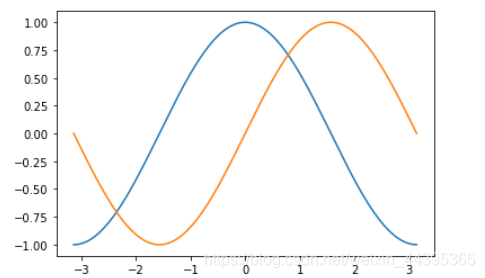
在这里插入图片描述




x=np.linspace(-pi,pi,256)
y,z=np.cos(x),np.sin(x)
plt.plot(x,y)
plt.plot(x,z)



绘图叠加


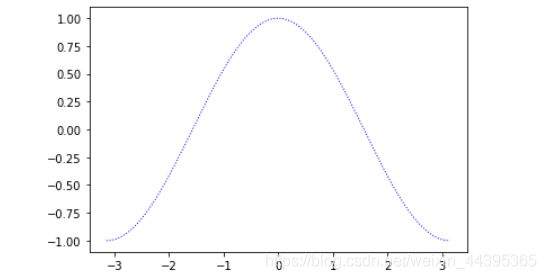
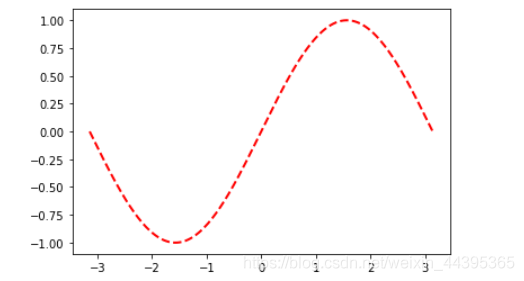
在这里插入图片描述



# 曲线颜色、标记、粗细
plot(x, y, color="blue", linewidth=1.0, linestyle=":")
plot(x,z,'--r',linewidth=2.0)



在这里插入图片描述

在这里插入图片描述



# 离散取值
a=np.arange(13)*pi/12
b=cos(3*a)
plot(a,b,'bo',markersize=3)



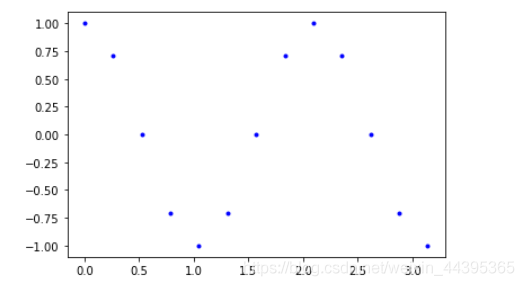
在这里插入图片描述



# 离散取值的属性及用虚线相连
a=np.arange(13)*pi/12
b=cos(3*a)
plot(a,b,'--rs',markeredgecolor='y',markerfacecolor='w')



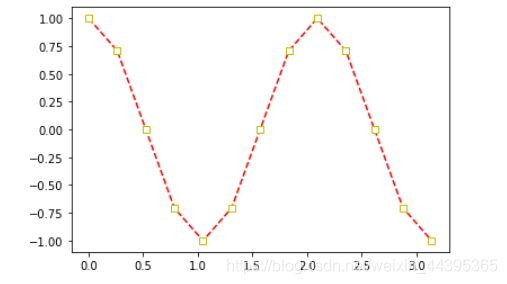
在这里插入图片描述



# 设置坐标轴的范围和记号
x=np.linspace(-pi,pi,256)
y,z=np.cos(x),np.sin(x)
xlim(-4,4)
xticks(np.linspace(-4,4,10))
ylim(-1.0,1.0)
yticks(np.linspace(-1.0,1.0,5))
plt.plot(x,y,'--r')




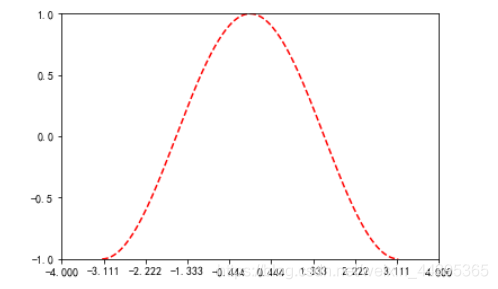
在这里插入图片描述



# 设置title与坐标轴的一些操作
# 设置中文
matplotlib.rcParams['axes.unicode_minus'] =False
plt.rcParams['font.sans-serif'] = ['SimHei']
x=np.linspace(-pi,pi,256)
y,z=np.cos(x),np.sin(x)
figure()
plt.plot(x,y)
axis('off')

figure()
plt.plot(x,z)
plt.xticks([])

plt.show()





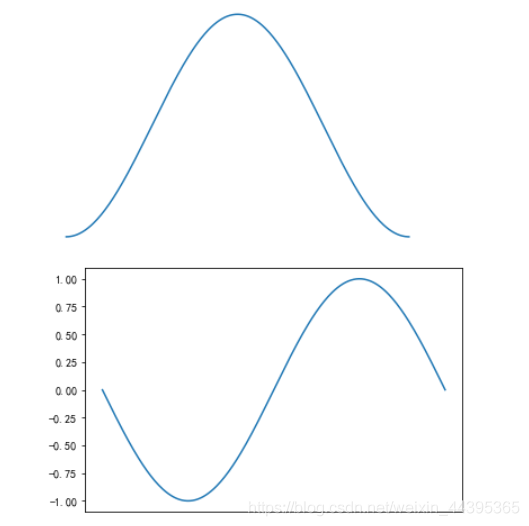
# 设置title与坐标轴的一些操作
# 设置中文
matplotlib.rcParams['axes.unicode_minus'] =False
plt.rcParams['font.sans-serif'] = ['SimHei']
x=np.linspace(-pi,pi,256)
y,z=np.cos(x),np.sin(x)
figure()
plt.plot(x,y)
axis('off')

figure()
plt.plot(x,z)
plt.xticks([])

plt.show()




在这里插入图片描述



#设置坐标轴的标签（多样化）
# xticks(locs, [labels], **kwargs)  # Set locations and labels **kwargs是关键字参数
import calendar

x = range(1,13,1)
y = range(1,13,1)
plt.plot(x,y)
# 标签手动设置（''，''，''，...）亦可
plt.xticks(x, calendar.month_name[1:13],color='m',rotation=45,fontsize=12,fontname='Arial')
plt.show()





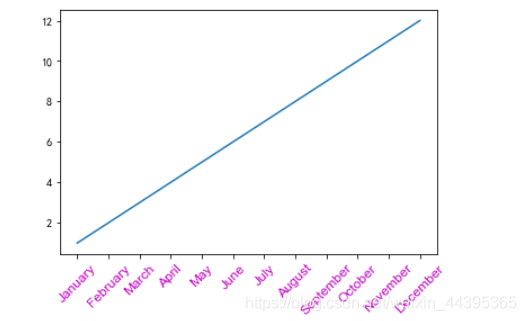
在这里插入图片描述



# 设置图例
matplotlib.rcParams['axes.unicode_minus'] =False

plt.rcParams['font.sans-serif'] = ['SimHei']
a=np.arange(13)*pi/12
b=cos(3*a)
plt.plot(a,b,'--rs',markeredgecolor='y',markerfacecolor='w',label='cos的图像')
xlabel('横轴')
ylabel('纵轴')
plt.legend(loc='upper right')
plt.show()




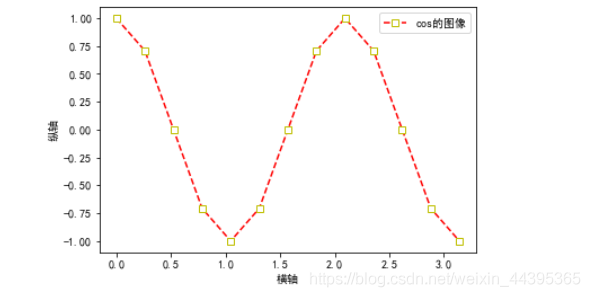
在这里插入图片描述



# 子图1
matplotlib.rcParams['axes.unicode_minus'] =False

x=np.linspace(-pi,pi,10)
y,z=np.cos(x),np.sin(x)
fig, (ax1 ,ax2) = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))
ax1.plot(x,y),ax2.plot(x,z)
ax1.set_title('cos'),ax2.set_title('sin')
plt.show()




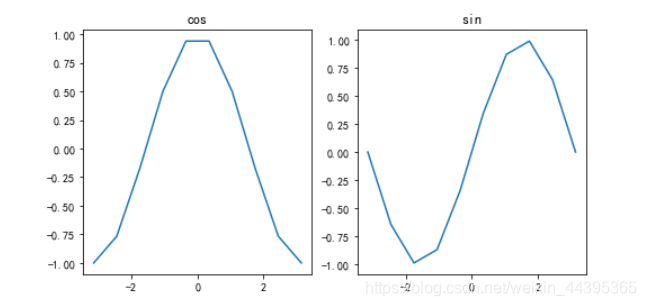
在这里插入图片描述



# 子图2
matplotlib.rcParams['axes.unicode_minus'] =False

x=np.linspace(-pi,pi,10)
y,z=np.cos(x),np.sin(x)
figure(figsize=(10,5),dpi=80)
subplot(121),plt.plot(x,y),plt.title('cos')
subplot(122),plt.plot(x,z),plt.title('sin')
plt.show()




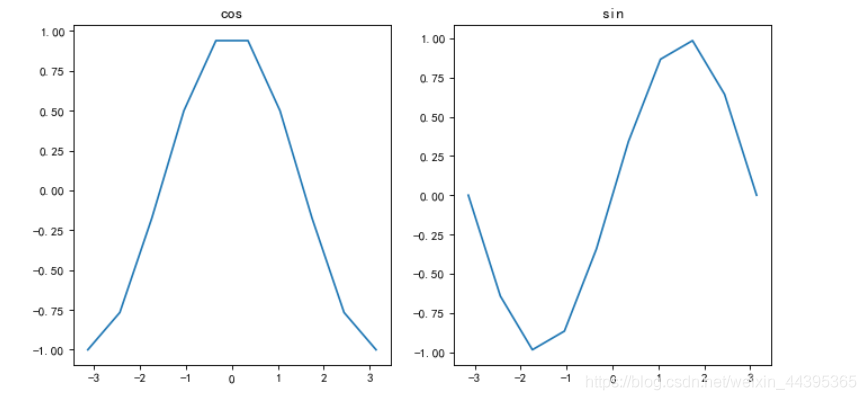
在这里插入图片描述


2.1 绘制实际图像中的点和线



# 使用matplotlib连线
from PIL import Image
from pylab import *

# 读取为列表，以便标记x、y的点？
im=array(Image.open('pic/kobe_mamba.jpg'))

imshow(im)

# 列表 包含四个点坐标
x=[100,100,400,400]
y=[200,500,200,500]

#红色叉型标出
plot(x,y,'rx')


# 连接坐标的前两个点的线 (100,200)与（100，500）
plot(x[:2],y[:2])

show()




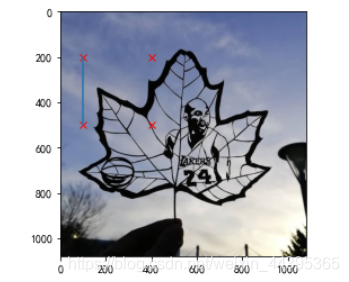
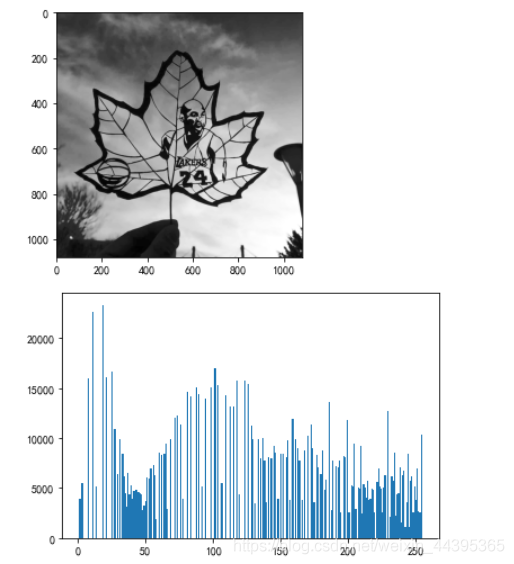
在这里插入图片描述


2.2 图像轮廓与直方图



# contour 与 hist
# 绘制轮廓要将图像先灰度化
from PIL import Image
from pylab import *

im=array(Image.open('pic/kobe_mamba.jpg').convert('L'))
figure()
# 
gray()
# 绘制轮廓,且起始位置从左上角开始
contour(im,origin='image')

# 坐标轴均匀分布
axis('equal')

# 新图像
figure()
hist(im.ravel(),256)

# hist的第二个参数指定小区间的个数，128个，即每个小区间灰度值跨度为2
figure()
hist(im.flatten(),128) 

show()




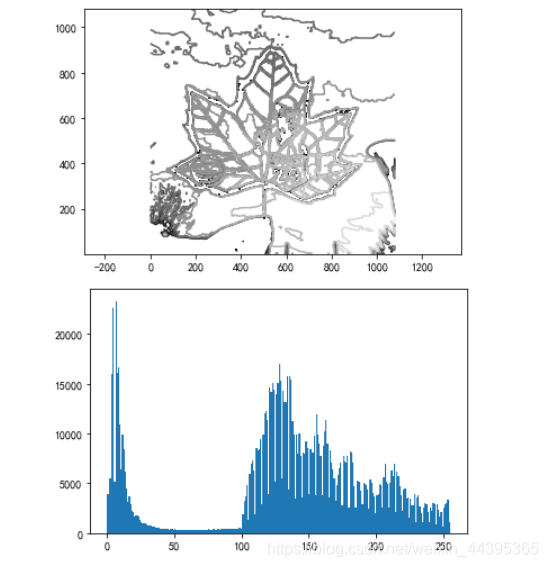
在这里插入图片描述


三、Numpy库基本学习



import numpy as np

import math
a=np.array(((1,2,3),(4,5,6)),dtype=float/complex)
a



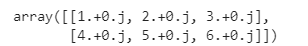
在这里插入图片描述

在这里插入图片描述



b=np.arange(15).reshape(3,5)
b
# 属性
b.shape
b.ndim
b.dtype
b.size
b.itemsize



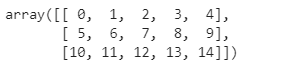
在这里插入图片描述



from numpy import pi
np.linspace( 0, 2, 9 )                 # 9 numbers from 0 to 2
array([ 0.  ,  0.25,  0.5 ,  0.75,  1.  ,  1.25,  1.5 ,  1.75,  2.  ])





c=np.random.random((2,3))

c.max/min()



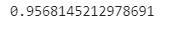
在这里插入图片描述



d=np.arange(12).reshape((3,4))
d.dtype.name
# 每个col的sum
print(d.sum(axis=0))
# 每行的累计和
print(d.cumsum(axis=1))



在这里插入图片描述



# 转变数组类型
a=np.array(((1,2,3),(4,5,6)),'float32')
a=a.astype('int16')
a



在这里插入图片描述



# 索引和切片
a = np.arange(10)**3 # 0~9的立方
a[2:5] #a[2-4]
# 令a[0,2,4]为-1000
a[:6:2] = -1000 
# reverse
a[ : :-1] 



在这里插入图片描述



a = np.arange(12).reshape((3,4))
a[0:3,1]
# 第2列
# or
a[:,1]
a[0:1,0:3]



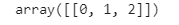
在这里插入图片描述



# 变换为1维数组
a = np.arange(12).reshape((3,4))
a.ravel()



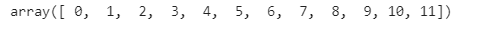
在这里插入图片描述



# 变换形状
a = np.arange(12).reshape((3,4))
a.resize((6,2))
a



在这里插入图片描述



a = np.arange(12).reshape((3,4))
b=10*np.random.random((3,4))
# 竖着叠加
np.vstack((a,b))
# 横着叠加
np.hstack((a,b))



在这里插入图片描述



x, y = np.ogrid[:3, :4]
# 同样可以设置步长
x, y = np.ogrid[0:3:1, 0:5:2]

# 询问,x>0的部分不变，其余赋值为2
np.where(x>0,x,2)



在这里插入图片描述


3.1 直方图均衡化



# 解释累加函数
import numpy as np
a=[1,2,3,4,5,6,7]
cdf=np.cumsum(a)

cdf[-1]

cdf=7*cdf/cdf[-1]
cdf




28


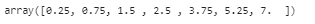
在这里插入图片描述



# 直方图均衡化
# bins 小区间的个数
def histeq(im,bins=256):
    #返回两个参数
    imhist,bins=histogram(im.flatten(),bins)
    # 累计分布函数，相当于cdf是一个列表
    cdf=imhist.cumsum()
    # cdf[-1]是列表的最后一个值，（0，255）
    cdf=255*cdf/cdf[-1]
    # 新的线性插值
    im2=interp(im.flatten(),bins[:-1],cdf)
    # 返回im2图像大小与im相同
    return im2.reshape(im.shape),cdf
# 直方图先转为灰度图
im=array(Image.open('pic/kobe_mamba.jpg').convert('L'))
im2,cdf=histeq(im,256)

figure()
imshow(im2)
figure()
hist(im2.flatten(),256)
show()




在这里插入图片描述


3.2 图像缩放



#  转换为array
img = np.asarray(image)

# 转换为Image
Image.fromarray(np.uint8(img))

# 图像缩放函数

def imresize(im,sz):
    # 将数组转换为图像
    pil_im=Image.fromarray(np.uint8(im))
    # 图像转换为数组
    return np.array(pil_im.resize(sz))

imshow(imresize(Image.open('pic/kobe_mamba.jpg'),(128,128)))




在这里插入图片描述


3.3 图像的主成分分析（PCA）




PCA（Principal Component Analysis，主成分分析）是一个非常有用的降维技巧。它可以在使用尽可能少维数的前提下，尽量多地保持训练数据的信息，在此意义上是一个最佳技巧。即使是一幅 100×100 像素的小灰度图像，也有 10 000 维，可以看成 10 000 维空间中的一个点。一兆像素的图像具有百万维。由于图像具有很高的维数，在许多计算机视觉应用中，我们经常使用降维操作。PCA 产生的投影矩阵可以被视为将原始坐标变换到现有的坐标系，坐标系中的各个坐标按照重要性递减排列。




为了对图像数据进行 PCA 变换，图像需要转换成一维向量表示。我们可以使用 NumPy 类库中的flatten() 方法进行变换。

将变平的图像堆积起来，我们可以得到一个矩阵，矩阵的一行表示一幅图像。在计算主方向之前，所有的行图像按照平均图像进行了中心化。我们通常使用 SVD（Singular Value Decomposition，奇异值分解）方法来计算主成分；但当矩阵的维数很大时，SVD 的计算非常慢，所以此时通常不使用 SVD 分解。





from PIL import Image
from numpy import *

def pca(X):
  """ 主成分分析：
    输入：矩阵X ，其中该矩阵中存储训练数据，每一行为一条训练数据
    返回：投影矩阵（按照维度的重要性排序）、方差和均值"""

  # 获取维数
    num_data,dim = X.shape

  # 数据中心化
    mean_X = X.mean(axis=0)
    X = X - mean_X

if dim>num_data:
  # PCA- 使用紧致技巧
  M = dot(X,X.T) # 协方差矩阵
  e,EV = linalg.eigh(M) # 特征值和特征向量
  tmp = dot(X.T,EV).T # 这就是紧致技巧
  V = tmp[::-1] # 由于最后的特征向量是我们所需要的，所以需要将其逆转
  S = sqrt(e)[::-1] # 由于特征值是按照递增顺序排列的，所以需要将其逆转
  for i in range(V.shape[1]):
    V[:,i] /= S
else:
  # PCA- 使用SVD 方法
  U,S,V = linalg.svd(X)
  V = V[:num_data] # 仅仅返回前nun_data 维的数据才合理

# 返回投影矩阵、方差和均值
return V,S,mean_X




四、Scipy


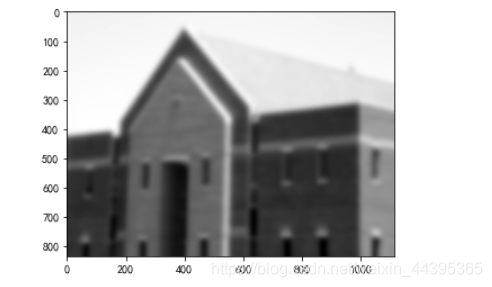
4.1 图像模糊



# 图像模糊
# Scipy 库
from PIL import Image
from numpy import *
from scipy.ndimage import filters

im=array(Image.open('pic/building.tif').convert('L'))
# filters.gaussian_filter第二个参数是标准差
im2=filters.gaussian_filter(im,9)
imshow(im2)




在这里插入图片描述



from PIL import Image
# 彩色通道，三通道分别进行高斯滤波
im=array(Image.open('pic/landmark500x500.jpg'))
im2=np.zeros((im.shape))
for i in arange(3):
    im2[:,:,i]=filters.gaussian_filter(im[:,:,i],2)
    
# 转换为(0，255)，否则imshow显示不出来
im2=uint8(im2)
figure(figsize=(5,5),dpi=80)
imshow(im2)
axis('off')





在这里插入图片描述


4.2 图像导数



from PIL import Image
from numpy import *
from scipy.ndimage import filters

# filters.sobel(src,0/1,dst),0表示y方向的方向导数，1表示x方向的方向导数

figure()
im=array(Image.open('pic/building.tif'))
imshow(im)


imx=np.zeros(im.shape)

imy=np.zeros(im.shape)
filters.sobel(im,0,imy)
figure()
imx=uint8(imy)
imshow(imy)

figure()
filters.sobel(im,1,imx)
imy=uint8(imx)
imshow(imx)

figure()
mag=sqrt(imx**2+imy**2)
mag=uint8(mag)
imshow(mag)

show()




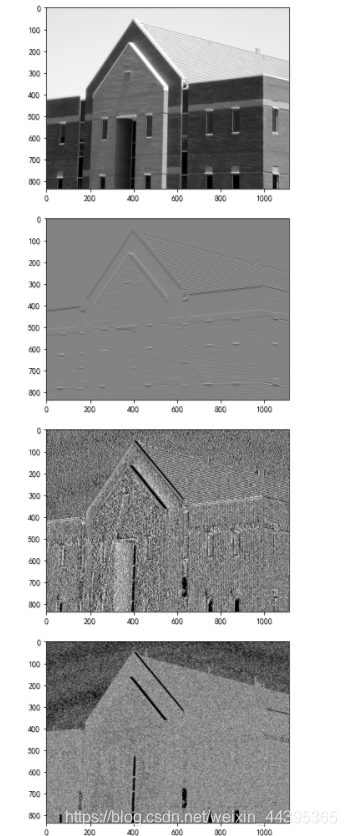
在这里插入图片描述


第二/三张图是sobel算子在x/y方向的导数，第四张图是两个导数叠加成梯度。


4.3 形态学计数



# 形态学 对象计数
from scipy.ndimage import measurements,morphology

im=array(Image.open('pic/zhiwen.tif').convert('L'))
im2=np.zeros(im.shape)
im2=1*(im<128)

labels,nbr_objects=measurements.label(im2)

print(f"Number of objects is {nbr_objects}.")

labels=np.uint8(labels)
imshow(labels)

im_open=morphology.binary_opening(im2,ones((3,3)),1)
labels_open,nbr_objects_open=measurements.label(im_open)
print(f"Number of objects is {nbr_objects_open}.")

imshow(labels_open)




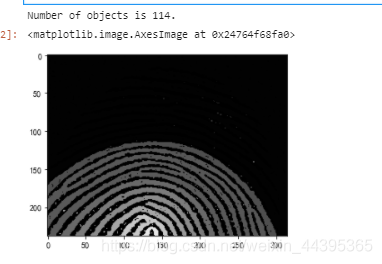
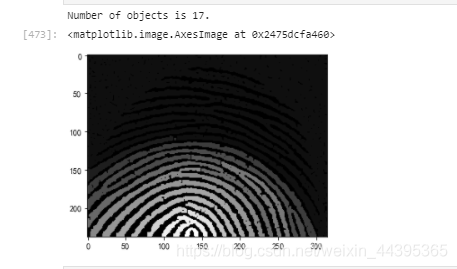
在这里插入图片描述

在这里插入图片描述


形态学计数使用label()函数，令图像的灰度值为标签，图一找到了114个物体，图二经过开操作，找到了17个物体。


到此这篇关于Python一些基本的图像操作和处理总结的文章就介绍到这了,更多相关Python图像操作和处理内容请搜索hwidc以前的文章或继续浏览下面的相关文章希望大家以后多多支持hwidc！

                            
                            【本文来源：高防服务器 转载请保留连接】

      
	  
  




 

  

    
 更多阅读