python实现A*寻路算法
目录
- A* 算法简介
- 关键代码介绍
- 保存基本信息的地图类
- 搜索到的节点类
- 算法主函数介绍
- 代码的初始化
- 完整代码
A* 算法简介
A* 算法需要维护两个数据结构:OPEN 集和 CLOSED 集。OPEN 集包含所有已搜索到的待检测节点。初始状态,OPEN集仅包含一个元素:开始节点。CLOSED集包含已检测的节点。初始状态,CLOSED集为空。每个节点还包含一个指向父节点的指针,以确定追踪关系。
A* 算法会给每个搜索到的节点计算一个G+H 的和值F:
- F = G + H
- G:是从开始节点到当前节点的移动量。假设开始节点到相邻节点的移动量为1,该值会随着离开始点越来越远而增大。
- H:是从当前节点到目标节点的移动量估算值。
- 如果允许向4邻域的移动,使用曼哈顿距离。
- 如果允许向8邻域的移动,使用对角线距离。
算法有一个主循环,重复下面步骤直到到达目标节点:
1 每次从OPEN集中取一个最优节点n(即F值最小的节点)来检测。
2 将节点n从OPEN集中移除,然后添加到CLOSED集中。
3 如果n是目标节点,那么算法结束。
4 否则尝试添加节点n的所有邻节点n'。
- 邻节点在CLOSED集中,表示它已被检测过,则无需再添加。
- 邻节点在OPEN集中:
- 如果重新计算的G值比邻节点保存的G值更小,则需要更新这个邻节点的G值和F值,以及父节点;
- 否则不做操作
- 否则将该邻节点加入OPEN集,设置其父节点为n,并设置它的G值和F值。
有一点需要注意,如果开始节点到目标节点实际是不连通的,即无法从开始节点移动到目标节点,那算法在第1步判断获取到的节点n为空,就会退出
关键代码介绍
保存基本信息的地图类
地图类用于随机生成一个供寻路算法工作的基础地图信息
先创建一个map类, 初始化参数设置地图的长度和宽度,并设置保存地图信息的二维数据map的值为0, 值为0表示能移动到该节点。
class Map(): def __init__(self, width, height): self.width = width self.height = height self.map = [[0 for x in range(self.width)] for y in range(self.height)]
在map类中添加一个创建不能通过节点的函数,节点值为1表示不能移动到该节点。
def createBlock(self, block_num): for i in range(block_num): x, y = (randint(0, self.width-1), randint(0, self.height-1)) self.map[y][x] = 1
在map类中添加一个显示地图的函数,可以看到,这边只是简单的打印出所有节点的值,值为0或1的意思上面已经说明,在后面显示寻路算法结果时,会使用到值2,表示一条从开始节点到目标节点的路径。
def showMap(self):
print("+" * (3 * self.width + 2))
for row in self.map:
s = '+'
for entry in row:
s += ' ' + str(entry) + ' '
s += '+'
print(s)
print("+" * (3 * self.width + 2))
添加一个随机获取可移动节点的函数
def generatePos(self, rangeX, rangeY): x, y = (randint(rangeX[0], rangeX[1]), randint(rangeY[0], rangeY[1])) while self.map[y][x] == 1: x, y = (randint(rangeX[0], rangeX[1]), randint(rangeY[0], rangeY[1])) return (x , y)
搜索到的节点类
每一个搜索到将到添加到OPEN集的节点,都会创建一个下面的节点类,保存有entry的位置信息(x,y),计算得到的G值和F值,和该节点的父节点(pre_entry)。
class SearchEntry(): def __init__(self, x, y, g_cost, f_cost=0, pre_entry=None): self.x = x self.y = y # cost move form start entry to this entry self.g_cost = g_cost self.f_cost = f_cost self.pre_entry = pre_entry def getPos(self): return (self.x, self.y)
算法主函数介绍
下面就是上面算法主循环介绍的代码实现,OPEN集和CLOSED集的数据结构使用了字典,在一般情况下,查找,添加和删除节点的时间复杂度为O(1), 遍历的时间复杂度为O(n), n为字典中对象数目。
def AStarSearch(map, source, dest):
...
openlist = {}
closedlist = {}
location = SearchEntry(source[0], source[1], 0.0)
dest = SearchEntry(dest[0], dest[1], 0.0)
openlist[source] = location
while True:
location = getFastPosition(openlist)
if location is None:
# not found valid path
print("can't find valid path")
break;
if location.x == dest.x and location.y == dest.y:
break
closedlist[location.getPos()] = location
openlist.pop(location.getPos())
addAdjacentPositions(map, location, dest, openlist, closedlist)
#mark the found path at the map
while location is not None:
map.map[location.y][location.x] = 2
location = location.pre_entry
我们按照算法主循环的实现来一个个讲解用到的函数。
下面函数就是从OPEN集中获取一个F值最小的节点,如果OPEN集会空,则返回None。
# find a least cost position in openlist, return None if openlist is empty def getFastPosition(openlist): fast = None for entry in openlist.values(): if fast is None: fast = entry elif fast.f_cost > entry.f_cost: fast = entry return fast
addAdjacentPositions 函数对应算法主函数循环介绍中的尝试添加节点n的所有邻节点n'。
# add available adjacent positions def addAdjacentPositions(map, location, dest, openlist, closedlist): poslist = getPositions(map, location) for pos in poslist: # if position is already in closedlist, do nothing if isInList(closedlist, pos) is None: findEntry = isInList(openlist, pos) h_cost = calHeuristic(pos, dest) g_cost = location.g_cost + getMoveCost(location, pos) if findEntry is None : # if position is not in openlist, add it to openlist openlist[pos] = SearchEntry(pos[0], pos[1], g_cost, g_cost+h_cost, location) elif findEntry.g_cost > g_cost: # if position is in openlist and cost is larger than current one, # then update cost and previous position findEntry.g_cost = g_cost findEntry.f_cost = g_cost + h_cost findEntry.pre_entry = location
getPositions 函数获取到所有能够移动的节点,这里提供了2种移动的方式:
- 允许上,下,左,右 4邻域的移动
- 允许上,下,左,右,左上,右上,左下,右下 8邻域的移动
def getNewPosition(map, locatioin, offset): x,y = (location.x + offset[0], location.y + offset[1]) if x < 0 or x >= map.width or y < 0 or y >= map.height or map.map[y][x] == 1: return None return (x, y) def getPositions(map, location): # use four ways or eight ways to move offsets = [(-1,0), (0, -1), (1, 0), (0, 1)] #offsets = [(-1,0), (0, -1), (1, 0), (0, 1), (-1,-1), (1, -1), (-1, 1), (1, 1)] poslist = [] for offset in offsets: pos = getNewPosition(map, location, offset) if pos is not None: poslist.append(pos) return poslist
isInList 函数判断节点是否在OPEN集 或CLOSED集中
# check if the position is in list def isInList(list, pos): if pos in list: return list[pos] return None
calHeuristic 函数简单得使用了曼哈顿距离,这个后续可以进行优化。
getMoveCost 函数根据是否是斜向移动来计算消耗(斜向就是2的开根号,约等于1.4)
# imporve the heuristic distance more precisely in future def calHeuristic(pos, dest): return abs(dest.x - pos[0]) + abs(dest.y - pos[1]) def getMoveCost(location, pos): if location.x != pos[0] and location.y != pos[1]: return 1.4 else: return 1
代码的初始化
可以调整地图的长度,宽度和不可移动节点的数目。
可以调整开始节点和目标节点的取值范围。
WIDTH = 10
HEIGHT = 10
BLOCK_NUM = 15
map = Map(WIDTH, HEIGHT)
map.createBlock(BLOCK_NUM)
map.showMap()
source = map.generatePos((0,WIDTH//3),(0,HEIGHT//3))
dest = map.generatePos((WIDTH//2,WIDTH-1),(HEIGHT//2,HEIGHT-1))
print("source:", source)
print("dest:", dest)
AStarSearch(map, source, dest)
map.showMap()
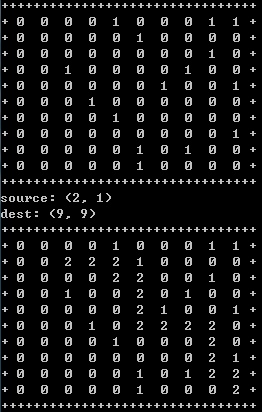
执行的效果图如下,第一个表示随机生成的地图,值为1的节点表示不能移动到该节点。
第二个图中值为2的节点表示找到的路径。
完整代码
使用python3.7编译
from random import randint
class SearchEntry():
def __init__(self, x, y, g_cost, f_cost=0, pre_entry=None):
self.x = x
self.y = y
# cost move form start entry to this entry
self.g_cost = g_cost
self.f_cost = f_cost
self.pre_entry = pre_entry
def getPos(self):
return (self.x, self.y)
class Map():
def __init__(self, width, height):
self.width = width
self.height = height
self.map = [[0 for x in range(self.width)] for y in range(self.height)]
def createBlock(self, block_num):
for i in range(block_num):
x, y = (randint(0, self.width-1), randint(0, self.height-1))
self.map[y][x] = 1
def generatePos(self, rangeX, rangeY):
x, y = (randint(rangeX[0], rangeX[1]), randint(rangeY[0], rangeY[1]))
while self.map[y][x] == 1:
x, y = (randint(rangeX[0], rangeX[1]), randint(rangeY[0], rangeY[1]))
return (x , y)
def showMap(self):
print("+" * (3 * self.width + 2))
for row in self.map:
s = '+'
for entry in row:
s += ' ' + str(entry) + ' '
s += '+'
print(s)
print("+" * (3 * self.width + 2))
def AStarSearch(map, source, dest):
def getNewPosition(map, locatioin, offset):
x,y = (location.x + offset[0], location.y + offset[1])
if x < 0 or x >= map.width or y < 0 or y >= map.height or map.map[y][x] == 1:
return None
return (x, y)
def getPositions(map, location):
# use four ways or eight ways to move
offsets = [(-1,0), (0, -1), (1, 0), (0, 1)]
#offsets = [(-1,0), (0, -1), (1, 0), (0, 1), (-1,-1), (1, -1), (-1, 1), (1, 1)]
poslist = []
for offset in offsets:
pos = getNewPosition(map, location, offset)
if pos is not None:
poslist.append(pos)
return poslist
# imporve the heuristic distance more precisely in future
def calHeuristic(pos, dest):
return abs(dest.x - pos[0]) + abs(dest.y - pos[1])
def getMoveCost(location, pos):
if location.x != pos[0] and location.y != pos[1]:
return 1.4
else:
return 1
# check if the position is in list
def isInList(list, pos):
if pos in list:
return list[pos]
return None
# add available adjacent positions
def addAdjacentPositions(map, location, dest, openlist, closedlist):
poslist = getPositions(map, location)
for pos in poslist:
# if position is already in closedlist, do nothing
if isInList(closedlist, pos) is None:
findEntry = isInList(openlist, pos)
h_cost = calHeuristic(pos, dest)
g_cost = location.g_cost + getMoveCost(location, pos)
if findEntry is None :
# if position is not in openlist, add it to openlist
openlist[pos] = SearchEntry(pos[0], pos[1], g_cost, g_cost+h_cost, location)
elif findEntry.g_cost > g_cost:
# if position is in openlist and cost is larger than current one,
# then update cost and previous position
findEntry.g_cost = g_cost
findEntry.f_cost = g_cost + h_cost
findEntry.pre_entry = location
# find a least cost position in openlist, return None if openlist is empty
def getFastPosition(openlist):
fast = None
for entry in openlist.values():
if fast is None:
fast = entry
elif fast.f_cost > entry.f_cost:
fast = entry
return fast
openlist = {}
closedlist = {}
location = SearchEntry(source[0], source[1], 0.0)
dest = SearchEntry(dest[0], dest[1], 0.0)
openlist[source] = location
while True:
location = getFastPosition(openlist)
if location is None:
# not found valid path
print("can't find valid path")
break;
if location.x == dest.x and location.y == dest.y:
break
closedlist[location.getPos()] = location
openlist.pop(location.getPos())
addAdjacentPositions(map, location, dest, openlist, closedlist)
#mark the found path at the map
while location is not None:
map.map[location.y][location.x] = 2
location = location.pre_entry
WIDTH = 10
HEIGHT = 10
BLOCK_NUM = 15
map = Map(WIDTH, HEIGHT)
map.createBlock(BLOCK_NUM)
map.showMap()
source = map.generatePos((0,WIDTH//3),(0,HEIGHT//3))
dest = map.generatePos((WIDTH//2,WIDTH-1),(HEIGHT//2,HEIGHT-1))
print("source:", source)
print("dest:", dest)
AStarSearch(map, source, dest)
map.showMap()
到此这篇关于python实现A*寻路算法的文章就介绍到这了,更多相关python A*寻路算法内容请搜索hwidc以前的文章或继续浏览下面的相关文章希望大家以后多多支持hwidc!
【本文转自:http://www.1234xp.com/jja.html 转载请说明出处】