K-means算法介绍

简单来说，K-means算法是一种无监督算法，不需要事先对数据集打上标签，即ground-truth，也可以对数据集进行分类，并且可以指定类别数目 牧师-村民模型

K-means 有一个著名的解释：牧师—村民模型：

有四个牧师去郊区布道，一开始牧师们随意选了几个布道点，并且把这几个布道点的情况公告给了郊区所有的村民，于是每个村民到离自己家最近的布道点去听课。
听课之后，大家觉得距离太远了，于是每个牧师统计了一下自己的课上所有的村民的地址，搬到了所有地址的中心地带，并且在海报上更新了自己的布道点的位置。
牧师每一次移动不可能离所有人都更近，有的人发现A牧师移动以后自己还不如去B牧师处听课更近，于是每个村民又去了离自己最近的布道点……
就这样，牧师每个礼拜更新自己的位置，村民根据自己的情况选择布道点，最终稳定了下来。

牧师的目的非常明显，就是要让每个来上自己课的村民走的路程最少

算法步骤

1. 指定k个中心点
2. 更新数据点所属类别：计算每个数据点到这k个点的欧氏距离，距离最小即为这个数据点的类别
3. 更新中心点坐标：对每一个类别的数据点求平均，平均值即为新的中心点位置

伪代码

获取m个n维的数据
随即选取k个点作为初始中心点
while keep_changing:
	for i in range(m):
		for j in range(k):
			计算每个点到center的距离
			判断离哪个点更近
		for center in range(k):
			更新类别中心点的坐标

用Python实现K-means聚类算法

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as datasets

def create_data():
    X,y = datasets.make_blobs(n_samples=1000,n_features=2,centers=[[1,0],[5,4],[2,3],[10,8],[7,4]])
    return X,y

def init_centers(data,k):
    m, n =data.shape
    # m 样本个数，n特征个数
    center_ids = np.random.choice(m,k)
    centers = data[center_ids]
    return centers

def cal_dist(ptA,ptB):
   return np.linalg.norm(ptA-ptB)

def kmeans_process(data,k):
    centers = init_centers(data, k)
    m, n = data.shape
    keep_changing = True
    pred_y = np.zeros((m,))

    while keep_changing:
        keep_changing = False
        # 计算剩余样本所属类别
        for i in range(m):
            min_distance = np.inf
            for center in range(k):
                distance = cal_dist(data[i,:],centers[center,:])
                if distance<min_distance: # 判断离哪个更近
                    min_distance = distance
                    idx = center # 类别换下
            if pred_y[i] != idx:   # 判断是否发生了改变
                keep_changing = True
            pred_y[i] = idx
        # 更新类别中心点坐标
        for center in range(k):
            cluster_data = data[pred_y==center]
            centers[center,:] = np.mean(cluster_data, axis=0) # 求相同类别数据点的质心点
        print(centers)
    return centers, pred_y

if __name__ == '__main__':
    X, y = create_data()
    centers , pred_y = kmeans_process(data=X, k=5)
    plt.scatter(X[:,0], X[:,1], s=3, c=pred_y)
    plt.scatter(centers[:,0], centers[:,1], s=10, c='k')
    plt.show()

效果图

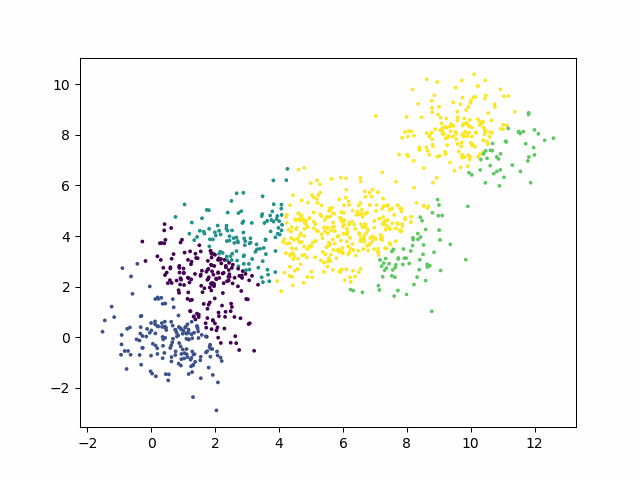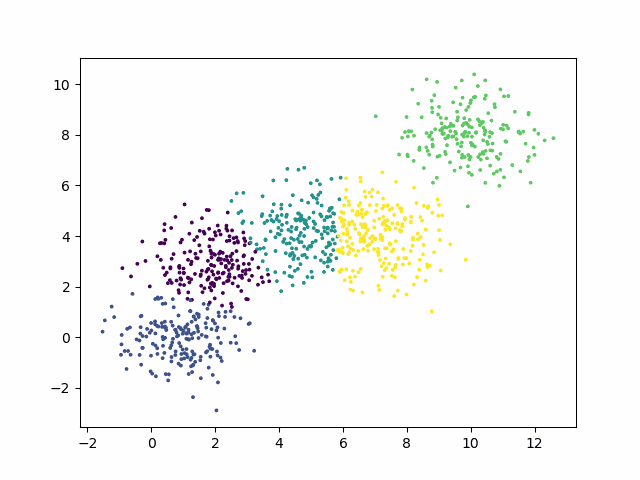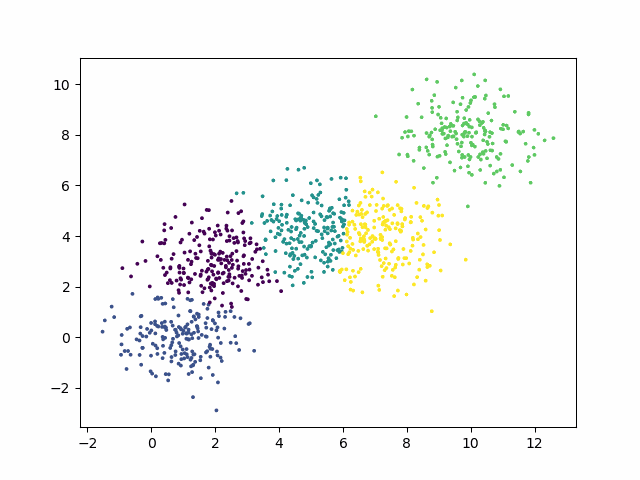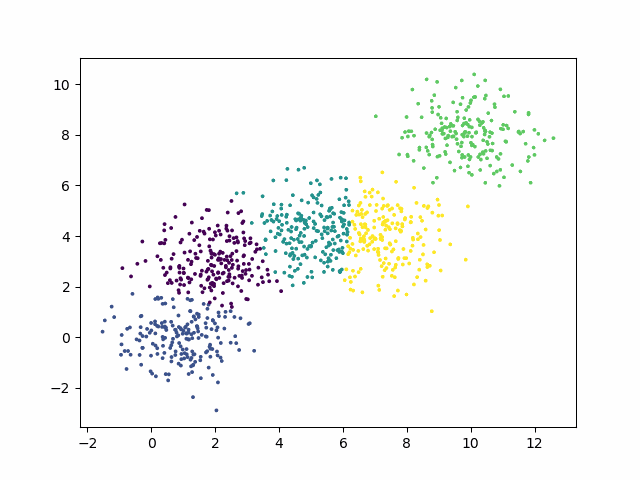
到此这篇关于Python实现K-means聚类算法并可视化生成动图步骤详解的文章就介绍到这了,更多相关Python可视化K-means聚类算法内容请搜索hwidc以前的文章或继续浏览下面的相关文章希望大家以后多多支持hwidc！