1.图和超图

图作为一种数据结构，由节点和边组成，可由下图表示。其中一个边只能链接两个节点。一个图可表示为G=（v，e，w）

其中v表示节点，e表示边，w表示节点的特征。关于图的表示可参考，本文不再详述。

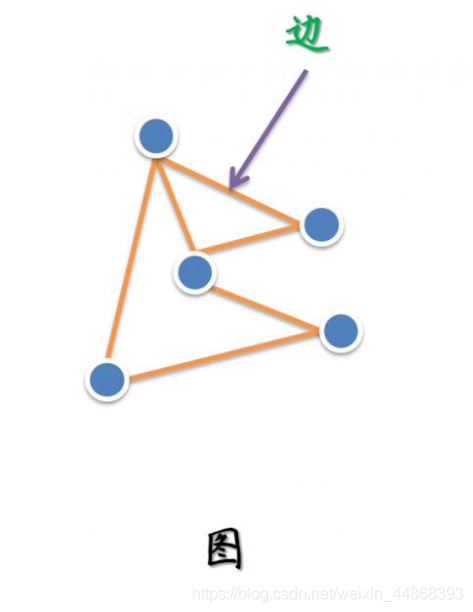
对于超图，其与图结构最主要的区别就是一条边可以连接多个节点，因此我们可以认为图是一种特殊的超图。超图结构如下图所示。

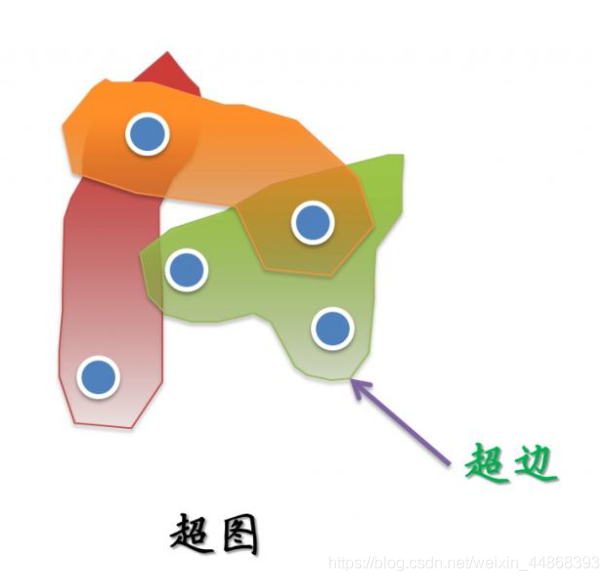
超图可表示为G=(υ,ε,ω)。其中υ为节点集合,ε为超边集合,ω为超边权重的对称矩阵。超图G可以关联矩阵H来表示，其词条定义为：

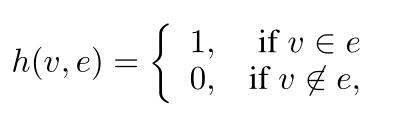
改公式可解释为如果某个节点属于某个超边，则关联矩阵H的值为1，否则为0。

对于单个节点v可定义为：

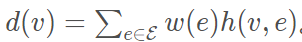
可解释为连接该节点的所有边乘上权重向量的和。

Dₑ和Dᵥ由d(v)和s(e)分别表示为超边和节点的对角矩阵。

单个边可定义为：

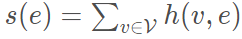
可以理解为该边包含的所有节点之和。

2.实例

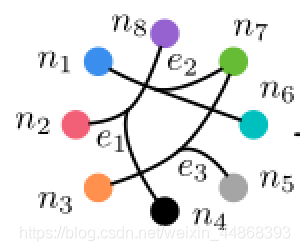
下面举出一个具体实例帮助理解超图的构建。以该图为例

图中有8个节点，3个超边。超边的细化图如下：

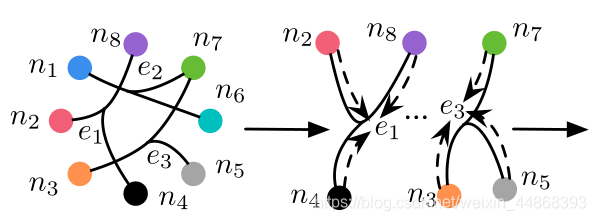
假设权重&W&为全1矩阵，因为它对构建超图数据结果无影响，那么H为一个3行8列的矩阵，表示为：

h(1,1) = 0

h(2,1) = 1

h(3,1) = 0

h(4,1) = 1

h(5,1) = 0

h(6,1) = 0

h(7,1) = 0

h(8,1) = 1

h(1,2) = 1

h(2,2) = 0

h(3,2) = 0

h(4,2) = 0

h(5,2) = 0

h(6,2) = 1

h(7,2) = 1

h(8,2) = 0

h(1,3) = 0

h(2,3) = 0

h(3,3) = 1

h(4,3) = 0

h(5,3) = 1

h(6,3) = 0

h(7,3) = 1

h(8,3) = 0

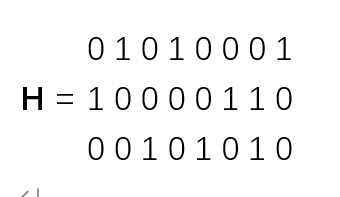
De​表示为：

d(1) = 1

d(2) = 1

d(3) = 1

d(4) = 1

d(5) = 1

d(6) = 1

d(7) = 2

d(8) = 1

Dv​表示为：

s(1) = 3

s(2) = 3

s(3) = 3

3.代码实现

下面我们用python代码进行编程，我们的目标是在知道节点的特征W通过特征的距离来生成 G \mathcal{G} G矩阵。路线为：W，H， G \mathcal{G} G。主要代码如下：

import numpy as np
#KNN生成H
x = np.array([[1,0,0,0,1,0,1,0,0,0],
        [1,1,1,0,0,0,1,1,1,0],
       [1,1,1,0,0,1,1,1,1,0],
       [0,1,0,0,0,0,1,0,1,0],
       [1,1,1,1,0,0,1,1,0,1],
       [1,0,1,0,0,1,0,1,1,0],
       [0,1,0,0,1,0,1,1,1,0],
       [0,1,1,0,1,0,1,0,1,1]])
def Eu_dis(x):
    """
    Calculate the distance among each raw of x
    :param x: N X D
                N: the object number
                D: Dimension of the feature
    :return: N X N distance matrix
    """
    x = np.mat(x)
    aa = np.sum(np.multiply(x, x), 1)
    ab = x * x.T
    dist_mat = aa + aa.T - 2 * ab
    dist_mat[dist_mat < 0] = 0
    dist_mat = np.sqrt(dist_mat)
    dist_mat = np.maximum(dist_mat, dist_mat.T)
    return dist_mat
def hyperedge_concat(*H_list):
    """
    Concatenate hyperedge group in H_list
    :param H_list: Hyperedge groups which contain two or more hypergraph incidence matrix
    :return: Fused hypergraph incidence matrix
    """
    H = None
    for h in H_list:
        if h is not None and h != []:
            # for the first H appended to fused hypergraph incidence matrix
            if H is None:
                H = h
            else:
                if type(h) != list:
                    H = np.hstack((H, h))
                else:
                    tmp = []
                    for a, b in zip(H, h):
                        tmp.append(np.hstack((a, b)))
                    H = tmp
    return H
def construct_H_with_KNN_from_distance(dis_mat, k_neig, is_probH=True, m_prob=1):
    """
    construct hypregraph incidence matrix from hypergraph node distance matrix
    :param dis_mat: node distance matrix
    :param k_neig: K nearest neighbor
    :param is_probH: prob Vertex-Edge matrix or binary
    :param m_prob: prob
    :return: N_object X N_hyperedge
    """
    n_obj = dis_mat.shape[0]
    # construct hyperedge from the central feature space of each node
    n_edge = n_obj
    H = np.zeros((n_obj, n_edge))
    for center_idx in range(n_obj):
        dis_mat[center_idx, center_idx] = 0
        dis_vec = dis_mat[center_idx]
        nearest_idx = np.array(np.argsort(dis_vec)).squeeze()
        avg_dis = np.average(dis_vec)
        if not np.any(nearest_idx[:k_neig] == center_idx):
            nearest_idx[k_neig - 1] = center_idx
        for node_idx in nearest_idx[:k_neig]:
            if is_probH:
                H[node_idx, center_idx] = np.exp(-dis_vec[0, node_idx] ** 2 / (m_prob * avg_dis) ** 2)
            else:
                H[node_idx, center_idx] = 1.0
    return H
def construct_H_with_KNN(X, K_neigs=[10], split_diff_scale=False, is_probH=True, m_prob=1):
    """
    init multi-scale hypergraph Vertex-Edge matrix from original node feature matrix
    :param X: N_object x feature_number
    :param K_neigs: the number of neighbor expansion
    :param split_diff_scale: whether split hyperedge group at different neighbor scale
    :param is_probH: prob Vertex-Edge matrix or binary
    :param m_prob: prob
    :return: N_object x N_hyperedge
    """
    if len(X.shape) != 2:
        X = X.reshape(-1, X.shape[-1])
    if type(K_neigs) == int:
        K_neigs = [K_neigs]
    dis_mat = Eu_dis(X)
    H = []
    for k_neig in K_neigs:
        H_tmp = construct_H_with_KNN_from_distance(dis_mat, k_neig, is_probH, m_prob)
        if not split_diff_scale:
            H = hyperedge_concat(H, H_tmp)
        else:
            H.append(H_tmp)
    return H
H = construct_H_with_KNN(x)
#生成G
def generate_G_from_H(H, variable_weight=False):
    """
    calculate G from hypgraph incidence matrix H
    :param H: hypergraph incidence matrix H
    :param variable_weight: whether the weight of hyperedge is variable
    :return: G
    """
    if type(H) != list:
        return _generate_G_from_H(H, variable_weight)
    else:
        G = []
        for sub_H in H:
            G.append(generate_G_from_H(sub_H, variable_weight))
        return G
def _generate_G_from_H(H, variable_weight=False):
    """
    calculate G from hypgraph incidence matrix H
    :param H: hypergraph incidence matrix H
    :param variable_weight: whether the weight of hyperedge is variable
    :return: G
    """
    H = np.array(H)
    n_edge = H.shape[1]
    # the weight of the hyperedge
    W = np.ones(n_edge)
    # the degree of the node
    DV = np.sum(H * W, axis=1)
    # the degree of the hyperedge
    DE = np.sum(H, axis=0)
    invDE = np.mat(np.diag(np.power(DE, -1)))
    DV2 = np.mat(np.diag(np.power(DV, -0.5)))
    W = np.mat(np.diag(W))
    H = np.mat(H)
    HT = H.T
    if variable_weight:
        DV2_H = DV2 * H
        invDE_HT_DV2 = invDE * HT * DV2
        return DV2_H, W, invDE_HT_DV2
    else:
        G = DV2 * H * W * invDE * HT * DV2
        return G
G = generate_G_from_H(H)

实验结果：

H

G

到此这篇关于如何建立一个超图的文章就介绍到这了,希望对你有帮助，更多相关超图内容请搜索hwidc以前的文章或继续浏览下面的相关文章，希望大家以后多多支持hwidc！