详细谈谈JS中的内存与变量存储
目录
- 前言
- JS神奇的Number
- 存储数字
- 二进制如何转换
- why 0.1 + 0.2 !== 0.3?
- 总结
前言
在前端领域,因为大部分在跟UI打交道,内存管理是最容易被忽略的部分。如果不懂内存,就看不清很多问题的本质,也难以写出更合格的代码,本次带大家走进内存的世界。
JS神奇的Number
案例一:金额的计算与传递
18.9 * 100 =1889.9999999999998
案例二:违背的数学定律
0.1 + 0.2 === 0.3
// false
(function (a, b, c) {
return a + b + c === a + ( b + c )
})(0.1, 0.2, 0.3)
// false
案例三:无限循环的加法
(function (num) {
while(true) {
if (++num % 13 === 0) {
return num
}
}
})(2 ** 53)
案例四:JSON.parse
JSON.parse('{"a":180143985094813214124}')
//{a: 180143985094813220000}
通过上面的四个案例我们可以看出,数字在计算机中运算往往会给人带来一些“惊喜”,要想防止这些意想不到的结果,我们首先要了解Number在Javascript中到底是怎么存储的?
存储数字
计算机是用二进制来存储数据的,所以数字也需要转换成相应二进制: 000 或者 111 的不同组合序列。
二进制如何转换
如何将一个数字转换成二进制,这里举个例子说明一下:
把十进制小数 106.6953125106.6953125106.6953125 转换成二进制
遇到小数转换时,需要把整数和小数两部分分别进行处理,整数 106106106 除以 222 直到商是 000 为止,取每次除 222 得到的余数结果
106 / 2 = 53 ...... 0 53 / 2 = 26 ...... 1 26 / 2 = 13 ...... 0 13 / 2 = 6 ...... 1 6 / 2 = 3 ...... 0 3 / 2 = 1 ...... 1 1 / 2 = 0 ...... 1 结果为得到的余数按照从右往左排列 1101010
小数 0.69531250.69531250.6953125 乘以 222 直到不存在小数位为止,并计下每次乘后的整数位结果,
0.6953125 x 2 = 1.390625 ...... 1 0.390625 x 2 = 0.78125【文章原创作者:http://www.1234xp.com/shsgf.html转载请保留出处】 ...... 0 0.78125 x 2 = 1.5625 ...... 1 0.5625 x 2 = 1.125 ...... 1 0.125 x 2 = 0.25 ...... 0 0.25 x 2 = 0.5 ...... 0 0.5 x 2 = 1 ...... 1 结果为得到的整数位按照从左往右排列 1011001
将计算后的 000 111 序列拼在一起就得到转换的二进制 1101010.10110011101010.10110011101010.1011001,用科学计数法表示为1.1010101011001∗261.1010101011001*2^61.1010101011001∗26,算出了二进制,接下来需要将它存进计算机中,在Javascript中不区分整数和小数,数字统一按照双精度浮点数的要求来存储,主要包含下面规则:
- 使用 8bytes(64bits)8bytes(64bits)8bytes(64bits) 存储双精度浮点数
- 存储小数用科学计数法表示的数据
- 第一位表示符号,后 111111 位表示指数,指数按照补位运算,即直接 102310231023 加指数位
- 剩余 525252 位表示小数点后的尾数,超过 525252 位的部分 000 舍 111 进
由于指数位的 11 位不包括符号位,那么为了达到正负指数的效果,就引入了指数的偏移值。
用图表示如下:

我们将转换好的二进制数按规则放进内存中,首先 106.6953125106.6953125106.6953125 是正数,所以符号位应该为 111, 000 表示正号, 111 表示负号(图片应该为显示 000,笔误了)

二进制 1.1010101011001∗261.1010101011001*2^61.1010101011001∗26 指数是 666(这里需要加上偏移量1023),转成二进制为 100000001011000000010110000000101,指数位要求放置二进制的补码,而补码的计算规则是:
- 正数的补码就是其本身
- 负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 [-1] = [10000001]原 = [11111110]反
所以图片指数位应该填

尾数位部分直接将小数转换后的二进制填入即可

数字最后就是以这样的形式存入计算机中
why 0.1 + 0.2 !== 0.3?
在理解数字存储的原理后,我们再来分析下为什么 0.1+0.2!==0.30.1 + 0.2 !== 0.30.1+0.2!==0.3
首先将 0.10.10.1 0.20.20.2 0.30.30.3 分别转换成二进制
0.1 x 2 = 0.2 ...... 0 0.2 x 2 = 0.4 ...... 0 0.4 x 2 = 0.8 ...... 0 0.8 x 2 = 1.6 ...... 1 0.6 x 2 = 1.2 ...... 1 0.2 x 2 = 0.4 ...... 0 0.4 x 2 = 0.8 ...... 0 0.8 x 2 = 1.6 ...... 1 0.6 x 2 = 1.2 ...... 1 得到的整数位按照从左往右排列 000110011...
0.1→0.00011(0011)∞
0.2 x 2 = 0.4 ...... 0 0.4 x 2 = 0.8 ...... 0 0.8 x 2 = 1.6 ...... 1 0.6 x 2 = 1.2 ...... 1 0.2 x 2 = 0.4 ...... 0 0.4 x 2 = 0.8 ...... 0 0.8 x 2 = 1.6 ...... 1 0.6 x 2 = 1.2 ...... 1 0.2 x 2 = 0.4 ...... 0 得到的整数位按照从左往右排列 001100110...
0.2→0.00110(0110)∞
0.3 x 2 = 0.6 ...... 0 0.6 x 2 = 1.2 ...... 1 0.2 x 2 = 0.4 ...... 0 0.4 x 2 = 0.8 ...... 0 0.8 x 2 = 1.6 ...... 1 0.6 x 2 = 1.2 ...... 1 0.2 x 2 = 0.4 ...... 0 0.4 x 2 = 0.8 ...... 0 0.8 x 2 = 1.6 ...... 1 得到的整数位按照从左往右排列 010011001...
0.3→0.01001(1001)∞
统一用科学计数法表示为
0.1→0.00011(0011)∞→1.(1001)∞∗2−4
0.2→0.00110(0110)∞→1.(1001)∞∗2−3
0.3→0.01001(1001)∞→1.(0011)∞∗2−2
放入计算机中双精度浮点数存储,最后的红色表示超过尾数位的二进制,即需要做舍0进1处理
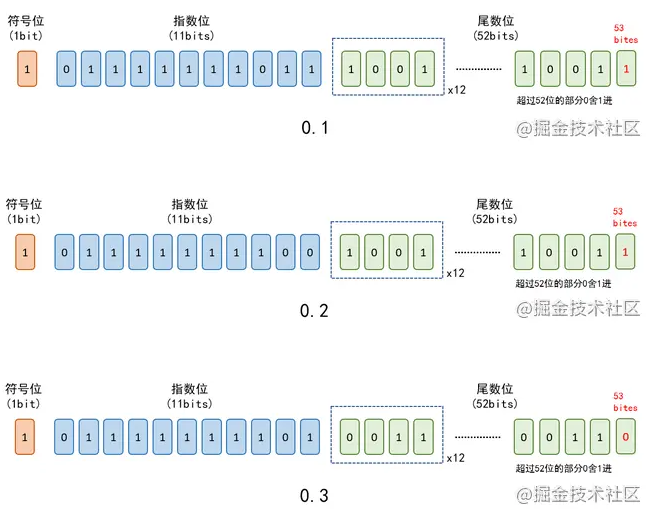
则经过64位双精度存储后,二进制如下表示
0.1→0−01111111011−(1001)121010
0.2→0−01111111100−(1001)121010
0.3→0−01111111101−(0011)120011
此时 0.1+0.20.1 + 0.20.1+0.2 可以看出与 0.30.30.3 不相等

这就是数字在计算机中运算往往会给人带来一些“惊喜”!
总结
到此这篇关于JS中内存与变量存储的文章就介绍到这了,更多相关JS内存与变量存储内容请搜索hwidc以前的文章或继续浏览下面的相关文章希望大家以后多多支持hwidc!
【文章转自:韩国cn2服务器 转载请保留连接】