python机器学习朴素贝叶斯算法及模型的选择和调

编辑: admin 分类: python 发布时间: 2021-12-03 来源:互联网

一、概率知识基础

1.概率

概率就是某件事情发生的可能性。

2.联合概率

包含多个条件，并且所有条件同时成立的概率，记作：P(A, B) = P(A) * P(B)

3.条件概率

事件A在另外一个事件B已经发生的条件下的发生概率，记作：P(A|B)

条件概率的特性：P(A1,A2|B) = P(A1|B)P(A2|B)

注意：此条件概率的成立，是由于A1,A2相互独立的结果

朴素贝叶斯的原理就是，对于每一个样本，算出属于每一个类别的概率，归为概率最高的那一类。

二、朴素贝叶斯

1.朴素贝叶斯计算方式

直接代入实际例子，各部分解释如下：

P(C) = P（科技）：科技文档类别的概率（科技文档数 / 总文档数）

P(W|C) = P（‘智能',‘发展'|科技）：在科技文档这一类文章中，‘智能'与‘发展'这两个特征词出现的概率。注意：‘智能'，‘发展'属于被预测文档中出现的词，科技文档中可能会有更多特征词，但给定的文档并不一定全部包含。因此，给定的文档包含了哪些，就使用哪些。

计算方法：

P(F1|C) = N(i)/N （训练集中计算）

N(i)是该F1词在C类别所有文档中出现的次数

N为所属类别C下的文档所有词出现的次数和

P（‘智能'|科技） = ‘智能'在所有科技类文档中出现的次数 / 科技类文档下所有出现的词次数和

则P(F1,F2...|C) = P(F1|C) * P(F2|C)

P（‘智能'，‘发展'|科技） = P（‘智能'|科技） * P（‘发展'|科技）

这样就可以计算出基于被预测文档中的特征词，被预测文档属于科技的概率。同样的方法计算其他类型的概率。哪个高就算哪个。

2.拉普拉斯平滑

3.朴素贝叶斯API

sklearn.naive_bayes.MultinomialNB

三、朴素贝叶斯算法案例

1.案例概述

本案例的数据是来自于sklearn中的20newsgroups数据，通过提取文章中的特征词，使用朴素贝叶斯方法，对被预测文章进行计算，通过得出的概率来确定文章属于哪一类。

大致步骤如下：首先将文章分成两类，一类作为训练集，一类作为测试集。接下来使用tfidf分别对训练集以及测试集文章进行特征抽取，这样就生成了训练集测试集的x，接下来可以直接调用朴素贝叶斯算法，将训练集数据x_train, y_train导入进去，训练模型。最后使用训练好的模型来测试即可。

2.数据获取

导入数据库：import sklearn.datasets as dt

导入数据：news = dt.fetch_20newsgroups(subset='all')

3.数据处理

分割使用的方法和knn中的一样。另外，从sklearn中导入的数据，都可以直接调用 .data获取数据集，调用.target获取目标值。

分割数据：x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)

特征值提取方法实例化：tf = TfIdfVectorizer()

训练集数据特征值提取：x_train = tf.fit_transform(x_train)

测试集数据特征值提取：x_test = tf.transform(x_test)

测试集的特征提取，只需要调用transform，因为要使用训练集的标准，并且在上一步已经fit过得出训练集的标准了，测试集直接使用就行。

4.算法流程

算法实例化：mlt = MultinomialNB(alpha=1.0)

算法训练：mlt.fit(x_train, y_train)

预测结果：y_predict = mlt.predict(x_test)

5.注意事项

朴素贝叶斯算法的准确率，是由训练集来决定的，不需要调参。训练集误差大，结果肯定不好。因为算的方式固定，并且没有一个超参数可供调整。

朴素贝叶斯的缺点：假设了文档中一些词和另外一些词是独立的，相互没联系。并且是在训练集中进行的词统计，会对结果造成干扰，训练集越好，结果越好，训练集越差，结果越差。

四、分类模型的评估

1.混淆矩阵

评估标准有数种，其一是准确率，也就是对预测的目标值和提供的目标值一一对比，计算准确率。

我们也有其他更通用也更好用的评估标准，即精确率和召回率。精确率和召回率是基于混淆矩阵计算的。

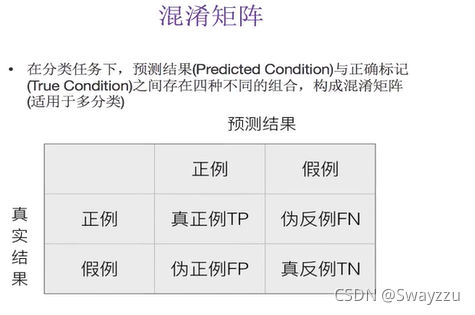
一般情况下我们只关注召回率。

F1分类标准：

根据以上式子，使用精确率召回率，可计算出F1-score，该结果可反应模型的稳健性。

2.评估模型API

sklearn.metricx.classification_report

3.模型选择与调优

①交叉验证

交叉验证是为了让被评估的模型更加准确可信，方法如下：

>>将所有数据分成n等份

>>第一份作为验证集，其他作为训练集，得出一个准确率，模型1

>>第二份作为验证集，其他作为训练集，得出一个准确率，模型2

>>......

>>直到每一份都过一遍，得出n个模型的准确率

>>对所有的准确率求平均值，我们就得到了最终更为可信的结果。

若分为四等分，则叫做“4折交叉验证”。

②网格搜索

网格搜索主要是和交叉验证同时使用，用来调参数。比如K-近邻算法中有超参数k，需要手动指定，比较复杂，所以需要对模型预设几种超参数组合，每组超参数都采用交叉验证来进行评估，最后选出最优的参数组合建立模型。（K-近邻算法就一个超参数k，谈不上组合，但是如果算法有2个或以上超参数，就进行组合，相当于穷举法）

网格搜索API：sklearn.model_selection.GridSearchCV

五、以knn为例的模型调优使用方法

假设已经将数据以及特征处理好，并且得到了x_train, x_test, y_train, y_test，并且已经将算法实例化：knn = KNeighborsClassifier()

1.对超参数进行构造

因为算法中需要用到的超参数的名字就叫做'n_neighbors'，所以直接按名字指定超参数选择范围。若有第二个超参数，在后面添加字典元素即可。

params = {'n_neighbors':[5,10,15,20,25]}

2.进行网格搜索

输入的参数：算法（估计器），网格参数，指定几折交叉验证

gc = GridSearchCV(knn, param_grid=params, cv=5)

基本信息指定好后，就可以把训练集数据fit进去

gc.fit(x_train, y_train)

3.结果查看

网格搜索算法中，有数种方法可以查看准确率、模型、交叉验证结果、每一次交叉验证后的结果。

gc.score(x_test, y_test) 返回准确率

gc.best_score_ 返回最高的准确率

gc.best_estimator_ 返回最好的估计器（返回的时候会自动带上所选择的超参数）

以上就是python机器学习朴素贝叶斯及模型的选择和调优详解的详细内容，更多关于朴素贝叶斯及模型的选择和调优的资料请关注hwidc其它相关文章！

【本文由：http://www.1234xp.com/cdn.html 提供,感谢支持】

海外服务器