Java数据结构中堆的向下和向上调整解析

编辑: admin 分类: java 发布时间: 2021-12-03 来源:互联网
目录
  • 一、关于堆
    • 1.堆的概念
    • 2.堆的性质
    • 3.堆的存储方式
  • 二、堆的创建
    • 1.堆向下调整
    • 2.堆的创建
  • 三、向上调整

    一、关于堆

    JDK1.8中的PriortyQueue（优先级队列）底层使用了堆的数据结构，而堆实际就是在完全二叉树的基础之上进行了一些元素的调整。

    1.堆的概念

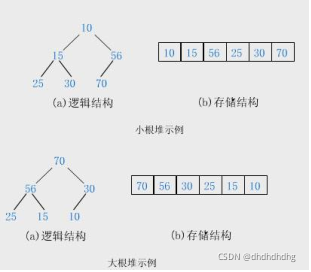
    堆有最大堆和最小堆之分。
    最大（最小）堆是一棵每一个节点的元素都不小于（大于）其孩子（如果存在）的元素的树。大堆是一棵完全二叉树，同时也是一棵最大树。小堆是一棵完全二叉树，同时也是一棵最小树。
    注意： 堆中的任一子树也是堆，即大堆的子树也都是大堆，小堆亦是。

    在这里插入图片描述

    2.堆的性质

    堆中某个结点的值总是不大于或不小于其父结点的值
    堆总是一颗完全二叉树

    3.堆的存储方式

    由堆的概念可知，堆是一颗完全二叉树，因此可以层序的规则采用顺序的方式来高效存储。
    注意：对于非完全二叉树，则不适合使用顺序方式进行存储，因为为了能够还原二叉树，空间中必须要能够存储空结点，就会导致空间利用率比较低

    二、堆的创建

    1.堆向下调整

    对于给出的一个数据，如何将其创建为堆呢？例如下图：

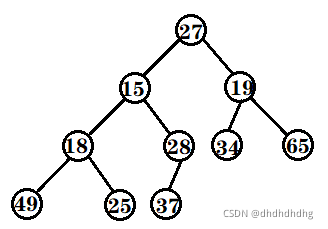
    在这里插入图片描述

    仔细观察上图后发现：根结点的左右子树已经完全满足堆的性质，因此只需将根结点向下调整好即可。
    以小堆为例：

    1.让parent标记需要调整的结点，child标记parent的左孩子（注意：parent如果有孩子一定是先有左孩子）
    2.如果parent的左孩子存在，即child<size，进行如下操作，直到parent的左孩子不存在

    parent右孩子是否存在，如果存在则找出左右孩子中较小的孩子，使用child进行标记
    将parent与较小的孩子（也就是此时的child）比较，如果：

    parent小于较小的孩子child，这个结点已经调整
    否则：将parent与child进行交换，交换成功后，这时parent中大的元素已经向下移动，可能会导致子树不满足堆的特性，就需要继续向下调整，即parent=child,child=parent*2+1,然后循环起来

    图解如下：

    在这里插入图片描述

    代码实现：

        private void shiftDown(int parent){
        //默认让child先标记左孩子---因为：parent可能有左没有右
        int child=parent*2+1;

        //while循环条件可以保证：parent的左孩子一定存在
        //             但是不能保证parent的右孩子是否存在
        while(child<size){
            //1.找到左右孩子中较小的孩子
            if(child+1<size&&array[child+1]<array[child]){
                child+=1;
            }

            //2.较小的孩子已经找到了
            //检测双亲和孩子之间是否满足堆的特性
            if(array[parent]>array[child]){
                swap(parent,child);

                //大的双亲往下走，可能会导致子树又不满足堆的特性
                //因此需要继续往下调整
                parent=child;
                child=parent*2+1;
            }else{
                //以parent为根的二叉树已经是堆了
                return;
            }
        }
    }

    注意： 在调整以parent为根的二叉树时，必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
    时间复杂度（看最坏的情况）： 从根一路比较到叶子，比较的次数为完全二叉树的高度，即时间复杂度为O(logn)。

    2.堆的创建

    向下调整的情况只能针对左右子树已经是堆了才可以调整，那假如根结点的左右子树不满足堆的特性，又该如何调整呢？例如下图：

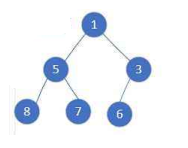
    在这里插入图片描述

    我们要从3这里的位置开始向下调整，然后逐渐向前依次向上调整
    3这个位置很特殊，他是二叉树倒数第一个非叶子结点
    步骤：

    1.找到倒数第一个非叶子结点
    2.从该结点位置开始往前一直到根结点，每遇到一个结点就使用向下调整

    代码实现：

    public static void createHeap(int[] array){
    //注意：倒数第一个非叶子节点刚好是最后一个节点的双亲
    //最后一个结点的编号是size-1，倒数第一个非叶子节点的下标为（size-1-1）/2
    int lastLeafParent=(size-2)/2;
    //从倒数第一个非叶子节点位置开始，一直到根节点的位置，使用向下调整
    for(int root=lastLeafParent;root>=0;root--){
       shiftDown(root);
    }
}

    建堆的时间复杂度：
    因为堆是完全二叉树，满二叉树也是完全二叉树，为了简化计算，此处使用满二叉树来证明：
    假设满二叉树高度h

    第一层：20个结点，需要向下移动h-1层
    第二层：21个结点，需要向下移动h-2层
    第二层：22个结点，需要向下移动h-3层
    …以此类推就可以求出所有的移动步数：每一层结点数与对应移动层数相乘再整体相加
    然后再利用一定的数学巧妙运算（此处省略那些繁琐的数学公式，属实是头大）就得出T(n)=n=log(n+1)≈n

    因此：建堆的时间复杂度为O(N)。

    三、向上调整

    向上调整主要的应用场景就是在堆的插入
    堆的插入总共需要两个步骤：

    1.先将元素插入到堆的末尾，即最后一个孩子之后
    2.插入后如果堆的性质遭到破坏，将最后新插入的节点向上调整，直到满足堆的性质

    在这里插入图片描述

    代码实现：

        private void shiftUp(int child){
        int parent=(child-1)/2;

        while(child!=0){
            if(array[child]<array[parent]){
                swap(child,parent);
                child=parent;
                parent=(child-1)/2;
            }else{
                return;
            }
        }
    }

    到此这篇关于Java数据结构中堆的向下和向上调整解析的文章就介绍到这了,更多相关Java 数据结构 内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！

    【本文由：http://www.1234xp.com/cdn.html 提供,感谢支持】
    更多阅读