Python与Matlab实现快速傅里叶变化的区别

编辑: admin 分类: python 发布时间: 2021-12-03 来源:互联网

注：两种语言的fft算法是有区别的，最后细聊！

Matlab的fftlw函数

输入是信号序列、对应的时间序列、以及是否作图，输出可以得到单边归一化之后的频率与对应的振幅，通过输出可以直接画出常用的频谱图！

function [ F,M ] = fftlw( x,y,draw )
%FFTLW 快速傅里叶变化2021.10.26
%输入   x--时间 y--信号 draw--1为画频谱图，0为不画
%输出   F--频率 M--幅值


N=length(y);                       %采样点数
if(mod(N,2)>0)
    N=N-1;
end
  
Fs=(N-1)/(x(N)-x(1));              %采样频率
F=(N/2:N-1)*Fs/N-Fs/2 ;            %频率
y2=abs(fftshift(fft(y(1:N))));     %快速傅里叶变化
M=2*y2(N/2+1:N)/N;                 %归一化
M(1)=M(1)/2;                       %常量除以2

if draw==1                         %可视化
    figure
    plot(F,M)
    xlabel('f/HZ')
    ylabel('amplitude')
    title('频谱图')
end
end

Python的fftlw函数

输入与matlab的略有点不同，分别是采样频率、信号序列、是否作图，输出与matlab的函数一致。

import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt

def fftlw(Fs,y,draw):
    '''
    Parameters
    ----------
    Fs : 采样频率
    y :  信号序列
    draw :1为画频谱图，0为不画 

    Returns
    -------
    f : 频率
    M : 幅值
    '''
    L=len(y)                              #采样点数
    f = np.arange(int(L / 2)) * Fs / L    #频率
    #M = np.abs(np.fft.fft(y))*2/L         #采用numpy.fft.fft()函数并归一化
    M = np.abs((fft(y))) *2/L             #采用scipy.fftpack.fft()函数并归一化
    M = M[0:int(L / 2)]                   #取单边谱
    M[0]=M[0]/2                           #常量除以2
    
    if draw==1:                           #可视化
        plt.figure()
        plt.rcParams['font.sans-serif']=['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        plt.plot(f,M)
        plt.xlabel('f/HZ')
        plt.ylabel('amplitude')
        plt.title('频谱图')
    return f,M

构造简单的信号对比两种语言fftlw效果

举个例子，构造如下信号验证所写函数的正确性：

y=3+t⋅sin(2πt⋅100)+3⋅sin(2πt⋅200)

其中，包括常数项，周期项和趋势项，理论上该信号的频率应该为0Hz、100Hz、200Hz（具体怎么算的补一补书知识）。在这里，我设置采样频率 fs=10000，产生10000个数据点，时域图如下：

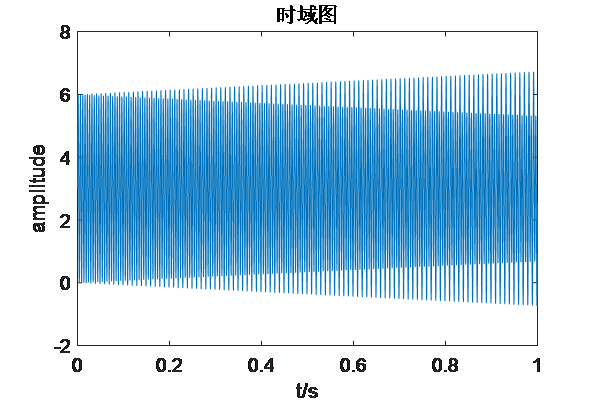
在这里插入图片描述

Matlab调用fftlw函数的主函数

fs=10000;                                     %采样频率
x=0:1/fs:(10000-1)/fs;                        %时间序列
y=sin(2*pi*x*100).*x+3*sin(2*pi*x*200)+3;     %信号序列
figure                                        %画时域图
plot(x,y)
title('时域图')
xlabel('t/s')
ylabel('amplitude')
[f,m]=fftlw(x,y,1);                           %快速傅里叶变化并画频谱图

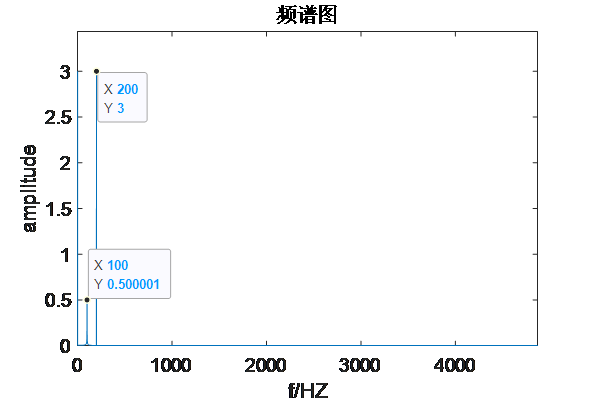
得到的频谱图如下：发现0Hz、100Hz、200Hz处的幅值分别为3，0.5，3。0Hz与200Hz处的幅值完美对应时域中常数项与s i n ( 2 π t ⋅ 200 ) 的系数；而100Hz项sin(2πt⋅200)的系数不是常数而是 t，且时间是0-1s，该项傅里叶变化得到的是该段时间内的平均幅值，也就是0.5。

在这里插入图片描述

Python调用fftlw函数的主函数
直接加在def fftlw()的后文调用他就行。

Fs=10000                #采用频率
L=10000                 #采样点数
t=np.arange(0,L/Fs,1/Fs)   #时间序列        
y=np.sin(2*np.pi*t*100)*t+3*np.sin(2*np.pi*t*200)+3  #信号序列
f,M=fftlw(Fs,y,1)         #快速傅里叶变化并画频谱图

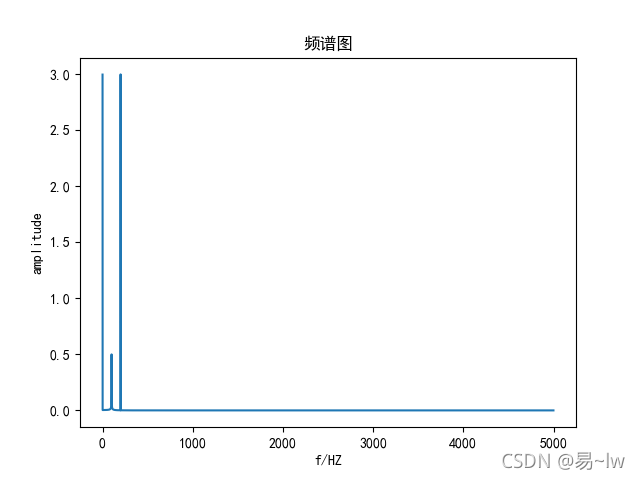
在这里插入图片描述

图和matlab的一模一样！但是！

采用实际的振动信号对比两种语言fftlw效果

数据来源于西储大学转子实验台振动信号，采样频率为12000Hz，现取正常状态下、转速1796 rpm轴承振动信号1000个点如下。粗略的观察，有一个低频信号大概周期为0.035 s，频率大概 29Hz。

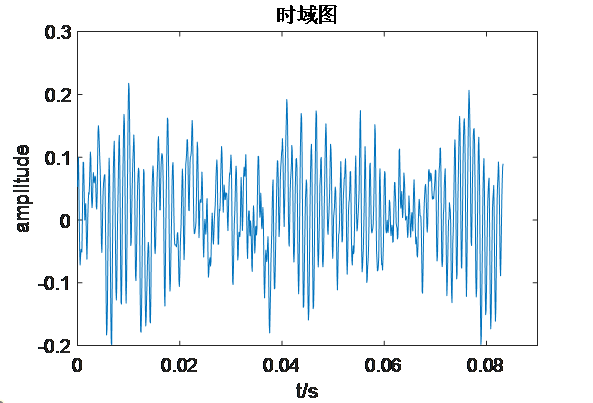
在这里插入图片描述

Matlab画频谱图

Matlab画频谱图

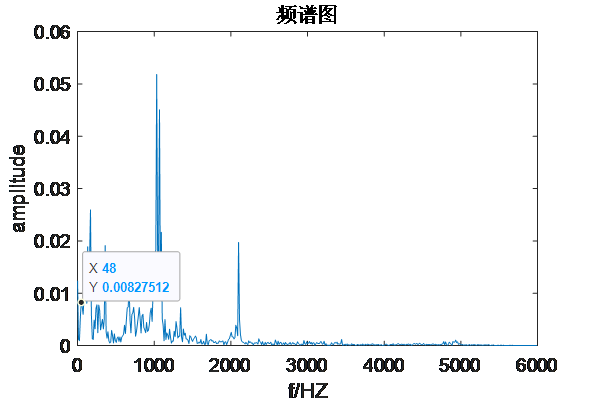
Python画频谱图

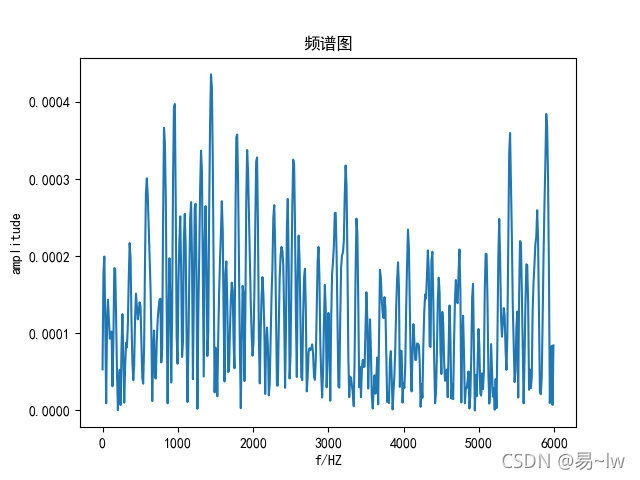
在这里插入图片描述

python的频谱图的幅值与原始数据量级差别较大，与matlab的频谱图也毫不相关，可能是底层傅里叶变换的算法不同所致，具体哪个正确还带进一步考证！！！

到此这篇关于Python与Matlab实现快速傅里叶变化的区别的文章就介绍到这了,更多相关Python 傅里叶变化内容请搜索hwidc以前的文章或继续浏览下面的相关文章希望大家以后多多支持hwidc！

【文章转自：韩国cn2服务器 转载请保留连接】
更多阅读