pyhthon绘制超炫酷的心形线星形线摆线

编辑: admin 分类: python 发布时间: 2021-12-03 来源:互联网
目录
  • 摆线
  • 外摆线和心脏线
  • 内摆线与星形线

摆线

最简单的旋轮线就是摆线，指圆在直线上滚动时，圆周上某定点的轨迹。

设圆的半径为 r ，在x轴上滚动  x距离则意味着旋转了 x \ r​ 弧度，则其滚动所产生的摆线如下

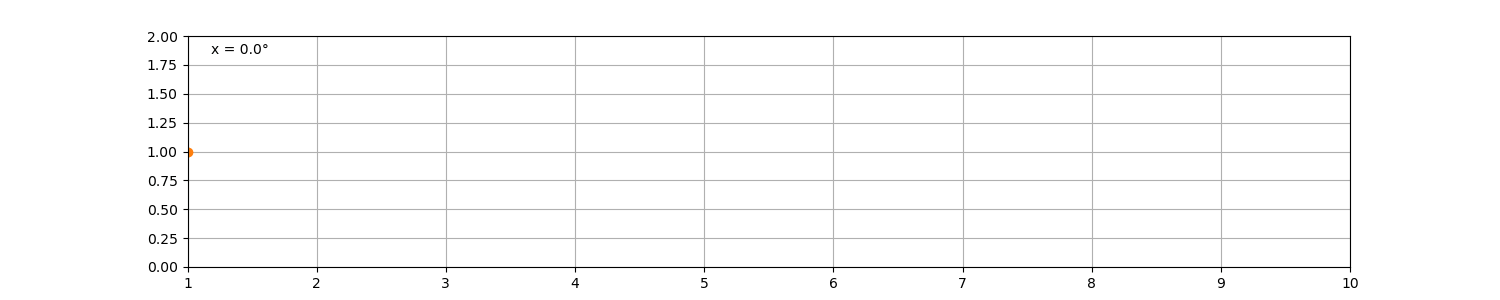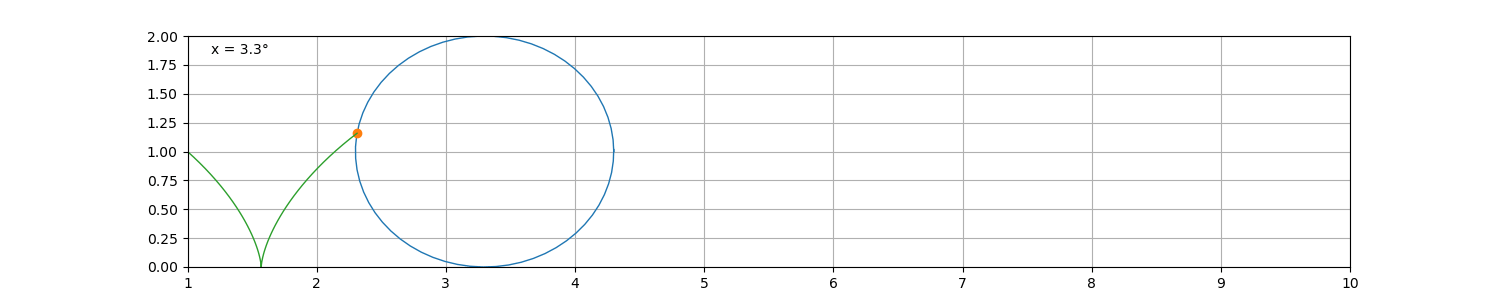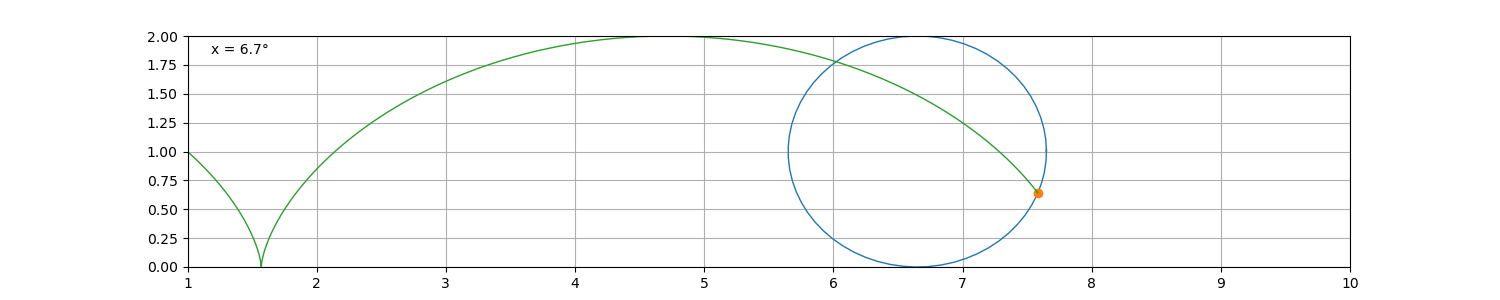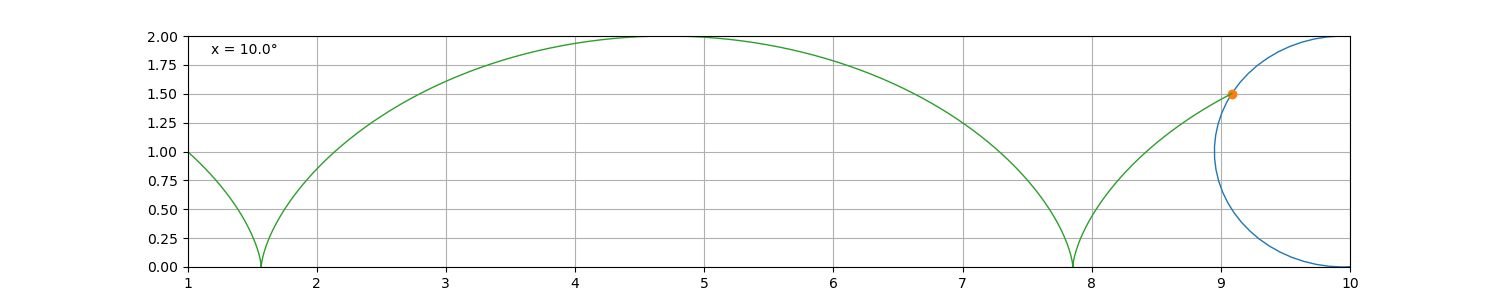
在这里插入图片描述

r = 1
theta = np.arange(0,6.4,0.1)
xCircle0 = np.cos(theta)
yCircle0 = 1+np.sin(theta)
fig = plt.figure(figsize=(15,4))
ax = fig.add_subplot(autoscale_on=False, 
    xlim=(1,10),ylim=(0,2))
ax.grid()
circle, = ax.plot(xCircle0,yCircle0,'-',lw=1)
point, = ax.plot([1],[1],'o')
trace, = ax.plot([],[],'-', lw=1)
theta_text = ax.text(0.02,0.85,'',transform=ax.transAxes)
textTemplate = '''x = %.1f°\n'''
xs,ys = [], []
def animate(x):
    if(x==0):
        xs.clear()
        ys.clear()
    xCycloid = x + r*np.cos(-x) #由于是向右顺时针滚，所以角度为负
    yCycloid = 1 + r*np.sin(-x)
    xCircle = xCircle0+x
    xs.append(xCycloid)
    ys.append(yCycloid)
    circle.set_data(xCircle,yCircle0)
    point.set_data([xCycloid],[yCycloid])
    trace.set_data(xs,ys)
    theta_text.set_text(textTemplate % x)
    return circle, point, trace, theta_text
frames = np.arange(0,10,0.02)
ani = animation.FuncAnimation(fig, animate, frames, 
    interval=5, blit=True)
ani.save("Cycloid.gif")
plt.show()

如果选取圆内或圆外的一点描成轨迹，则为次摆线，圆外点的轨迹为长幅摆线，

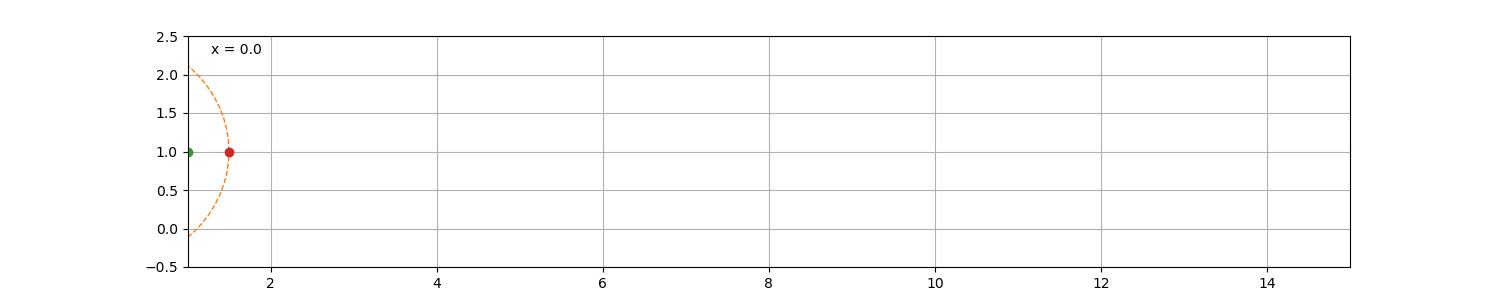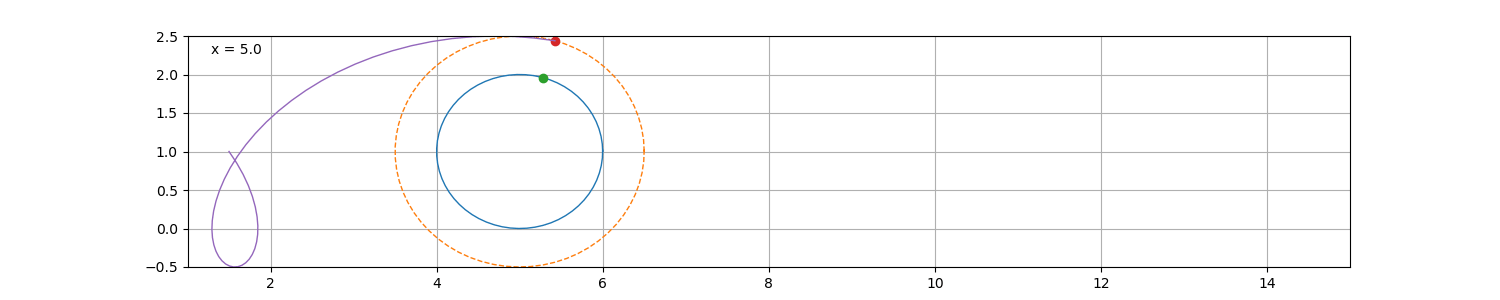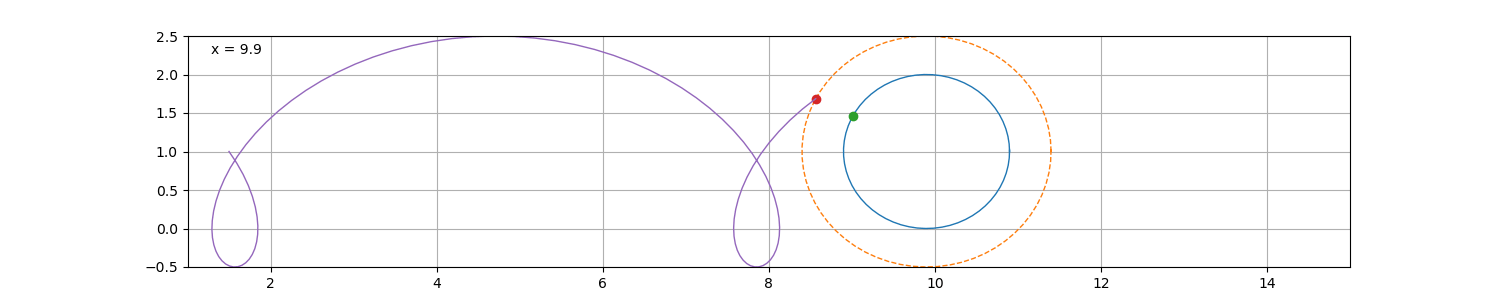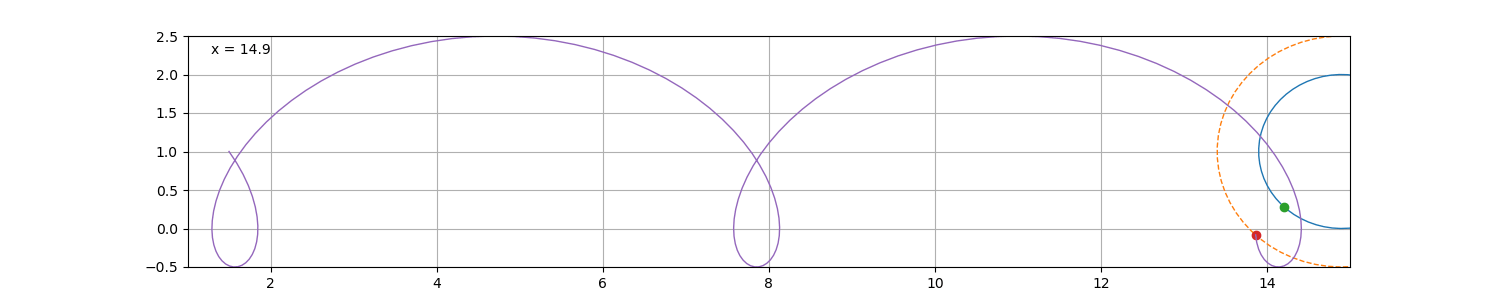
在这里插入图片描述

反之则为短幅摆线

在这里插入图片描述

代码

r = 1
rIn = 0.5
theta = np.arange(0,6.4,0.1)
xCircle0 = np.cos(theta)
yCircle0 = 1+np.sin(theta)
xCircleOut0 = rIn*np.cos(theta)
yCircleOut0 = 1+rIn*np.sin(theta)
fig = plt.figure(figsize=(20,3))
ax = fig.add_subplot(autoscale_on=False, 
    xlim=(1,15),ylim=(0,2))
ax.grid()
circle, = ax.plot(xCircle0,yCircle0,'-',lw=1)
circleOut, = ax.plot(xCircleOut0,yCircleOut0,linestyle='--',lw=1)
point, = ax.plot([1],[1],'o')
pointOut, = ax.plot([1],[1.5],'o')
trace, = ax.plot([],[],'-', lw=1)
theta_text = ax.text(0.02,0.85,'',transform=ax.transAxes)
textTemplate = '''x = %.1f\n'''
xs,ys = [], []
def animate(x):
    if(x==0):
        xs.clear()
        ys.clear()
    xCycloid = x + r*np.cos(-x)
    yCycloid = 1 + r*np.sin(-x)
    xCycloidOut = x + rIn*np.cos(-x)
    yCycloidOut = 1 + rIn*np.sin(-x)
    xs.append(xCycloidOut)
    ys.append(yCycloidOut)
    circle.set_data(xCircle0+x,yCircle0)
    circleOut.set_data(xCircleOut0+x,yCircleOut0)
    point.set_data([xCycloid],[yCycloid])
    pointOut.set_data([xCycloidOut],[yCycloidOut])
    trace.set_data(xs,ys)
    theta_text.set_text(textTemplate % x)
    return circle, circleOut, point, pointOut, trace, theta_text
frames = np.arange(0,15,0.1)
ani = animation.FuncAnimation(fig, animate, frames, 
    interval=50, blit=True)
ani.save("Cycloid.gif")
plt.show()

在这里插入图片描述

随着 λ 的变化，图像的变化过程为

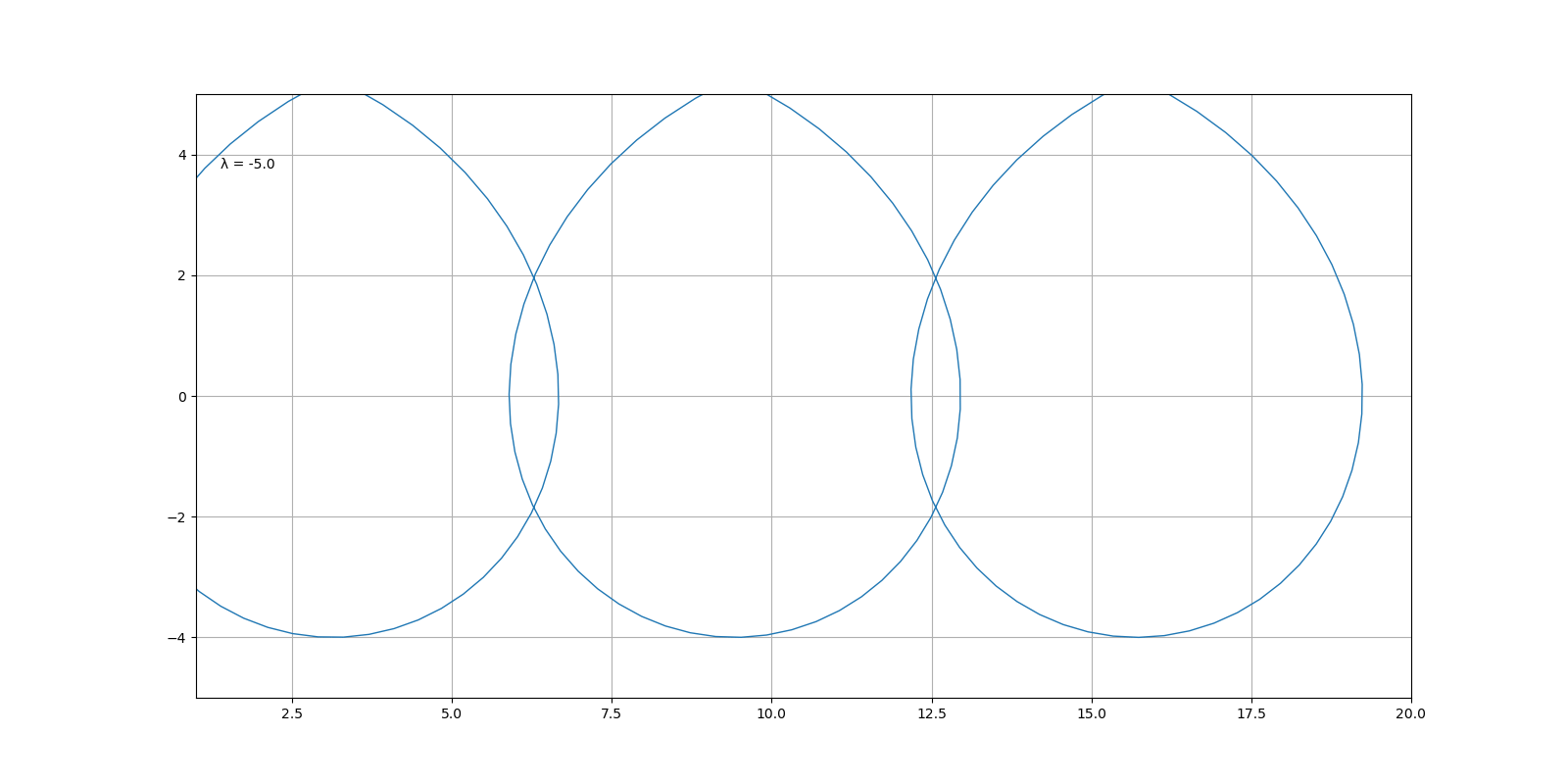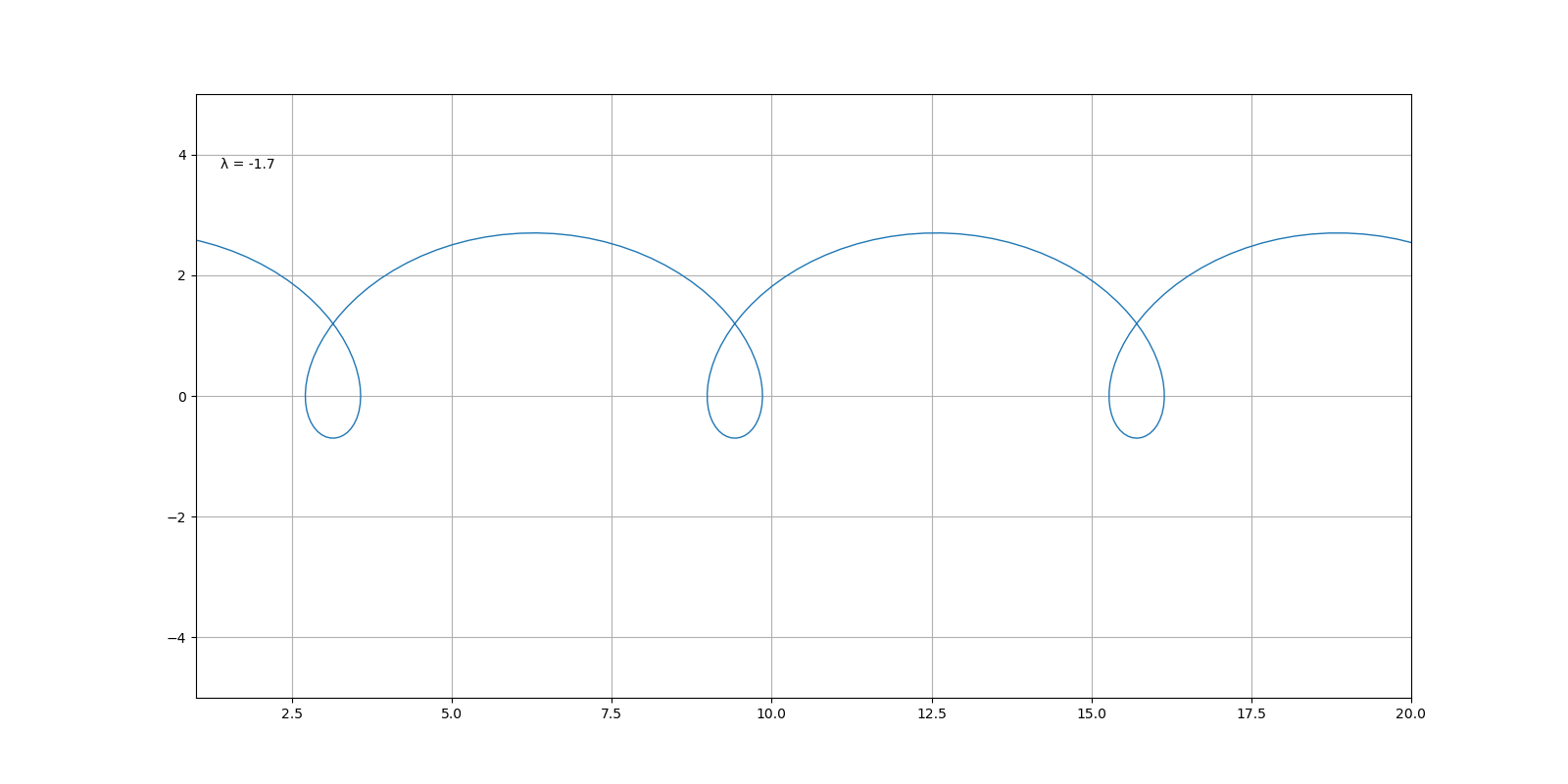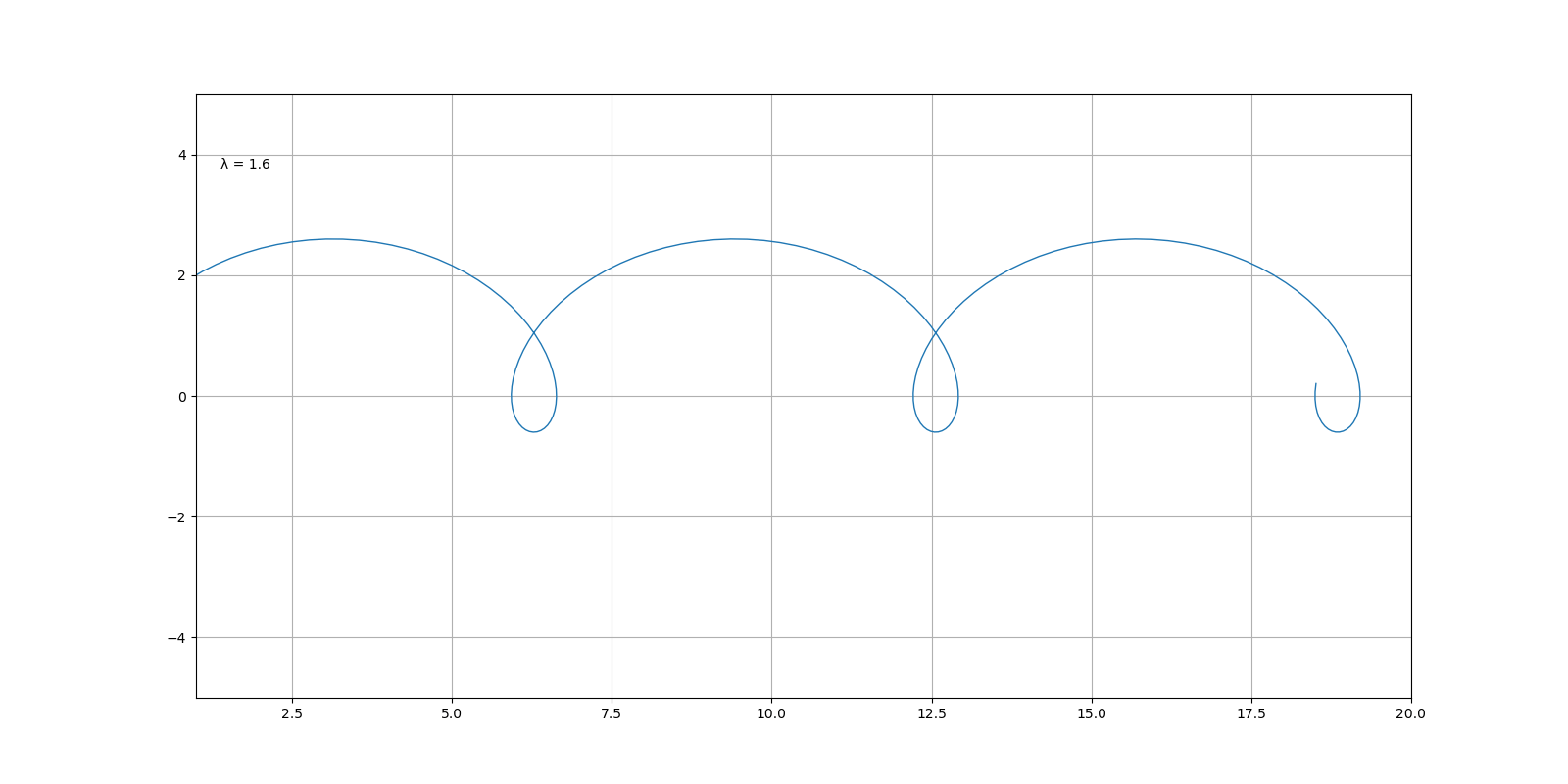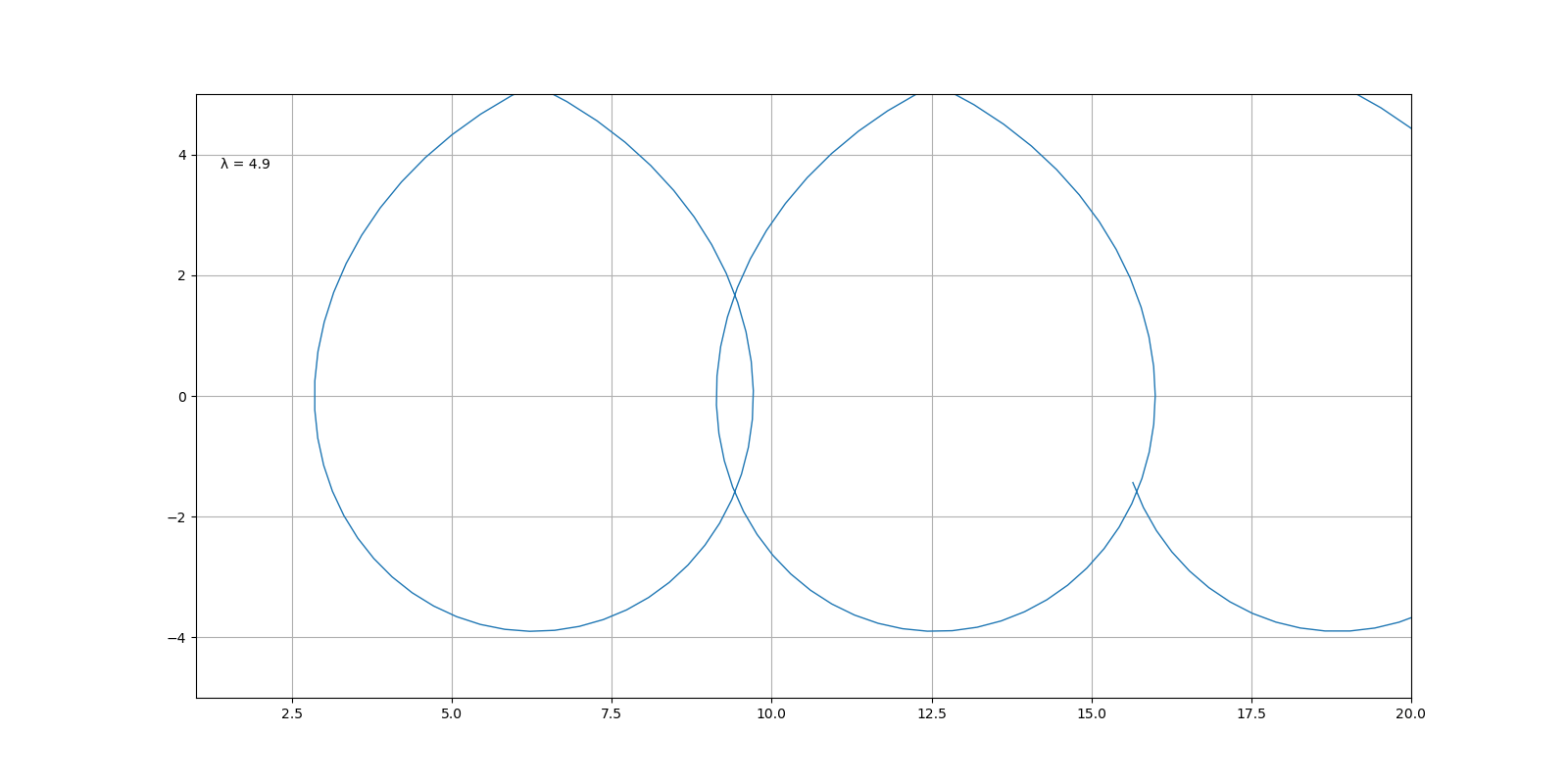
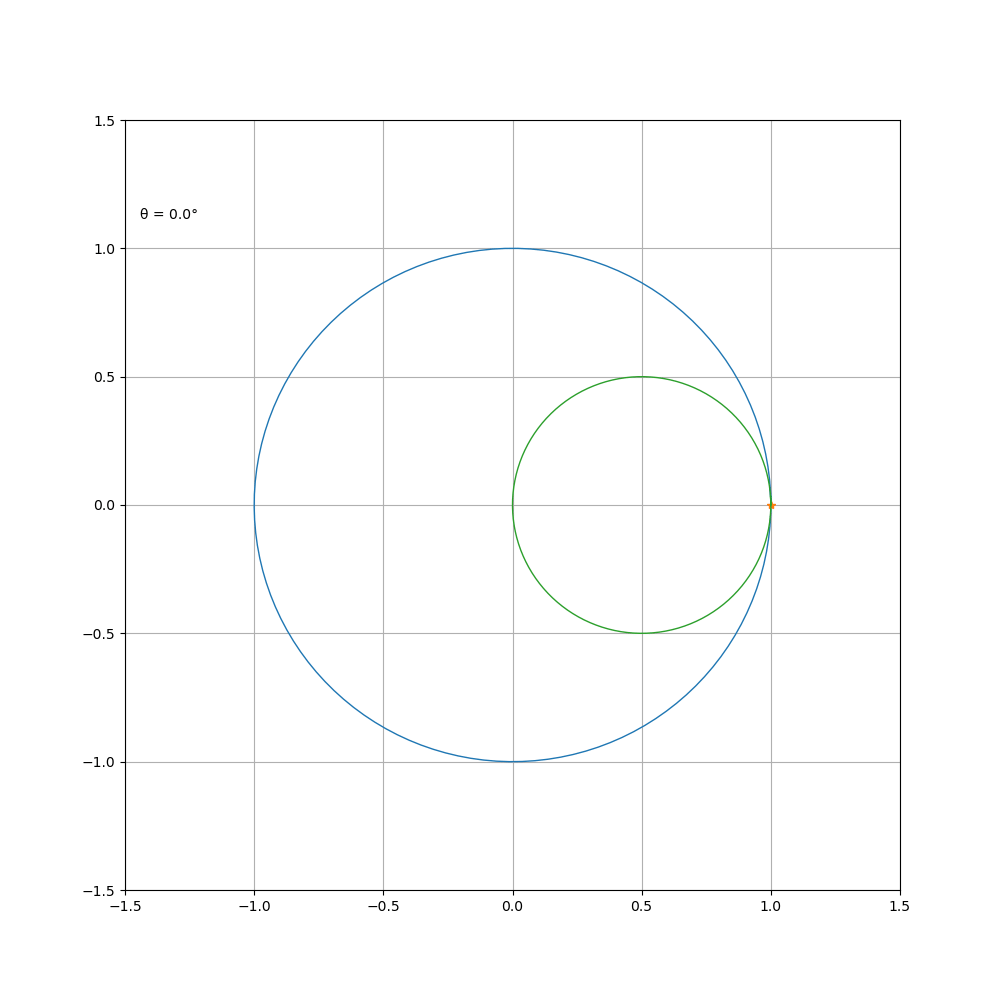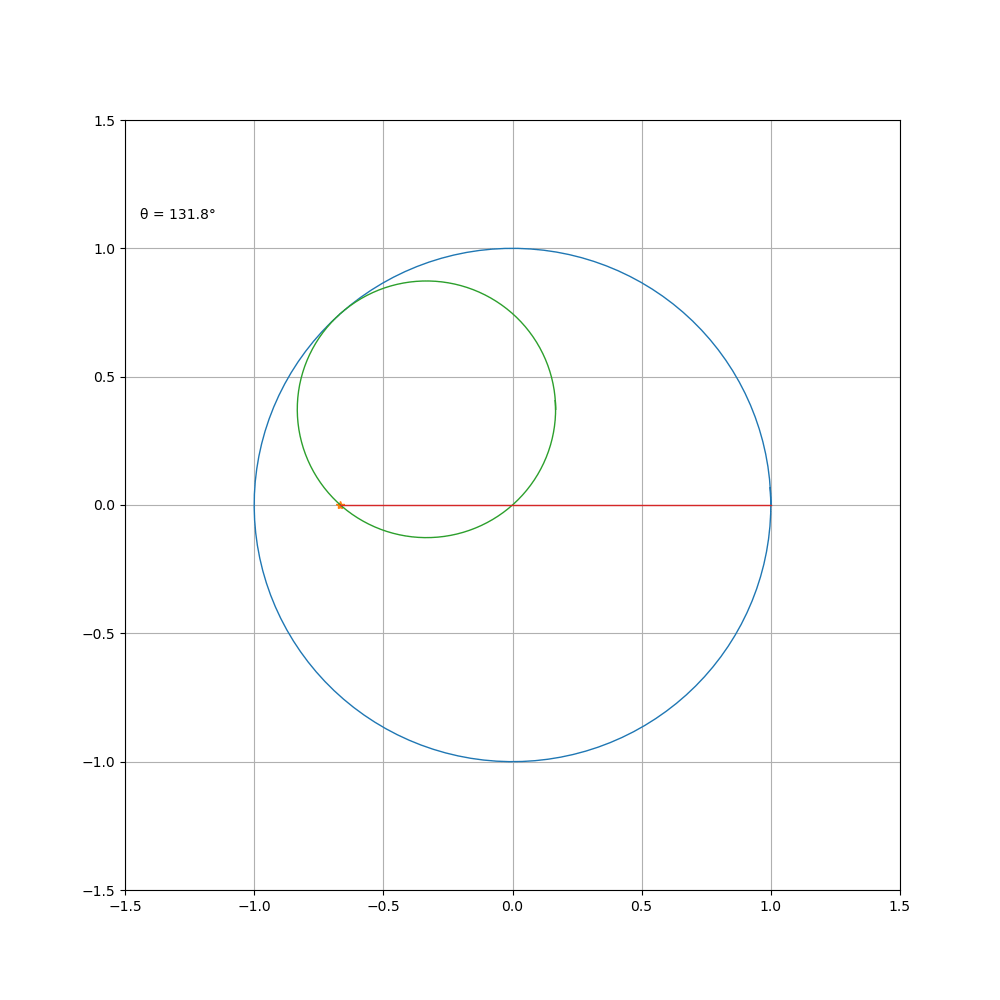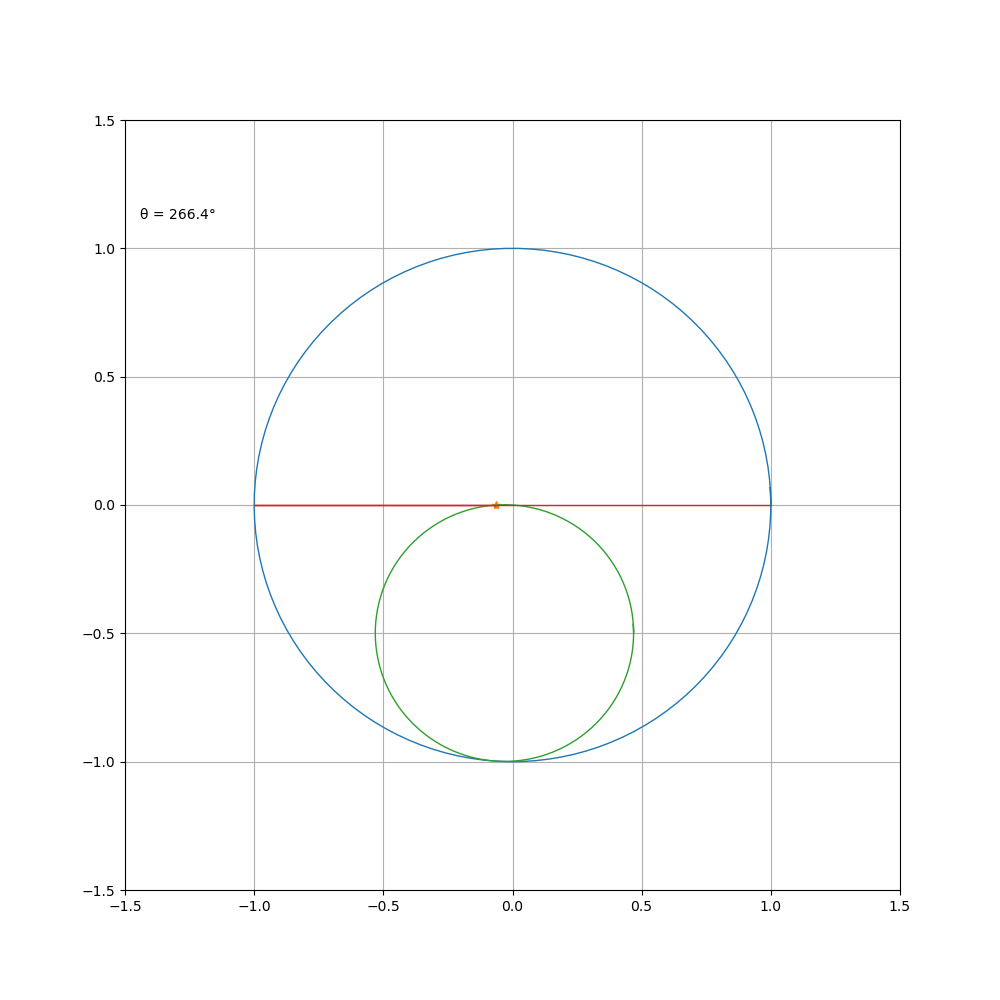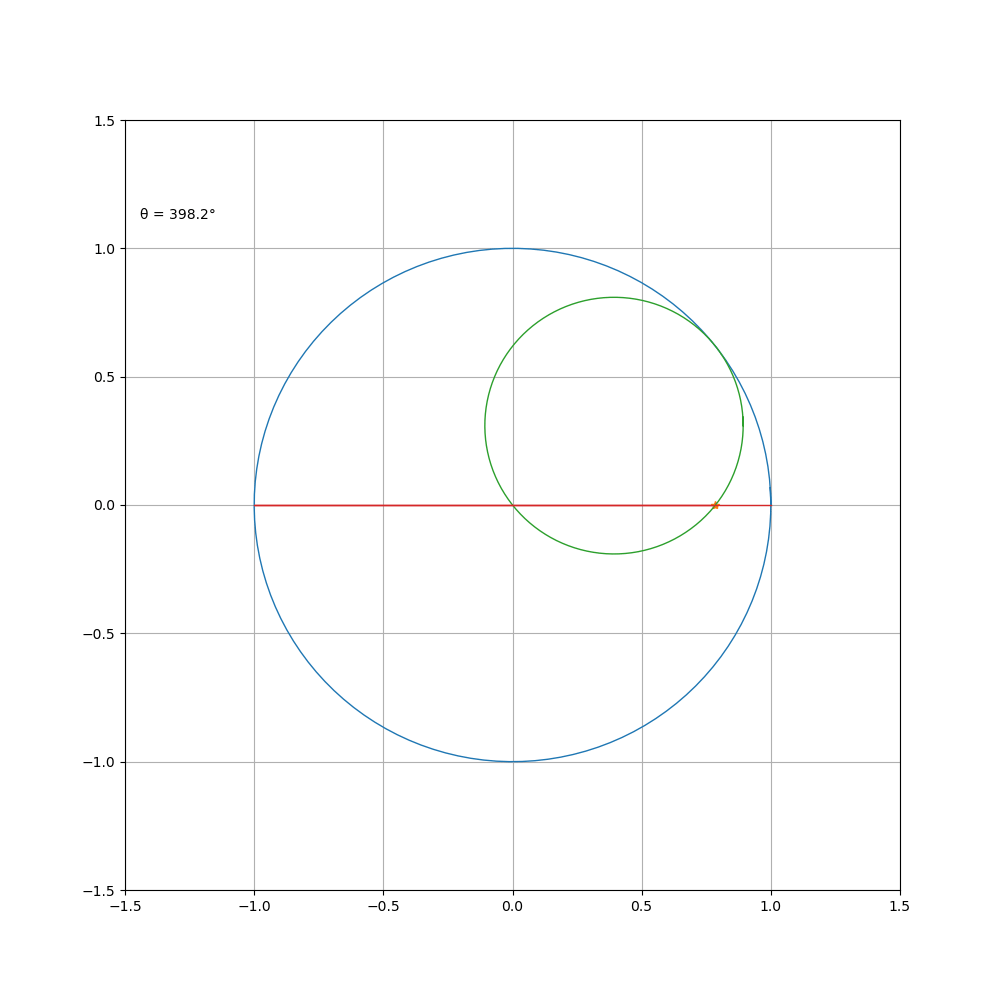
在这里插入图片描述

外摆线和心脏线

如果在一个圆绕着另一个固定的圆滚动，如果在圆外滚动，则动圆上的某相对固定点的轨迹为外摆线；若在圆内滚动，则某点的轨迹为内摆线。设定圆半径为 a ，动圆半径为 b ，则绕行旋转  t度后，动圆圆心圆心位置为

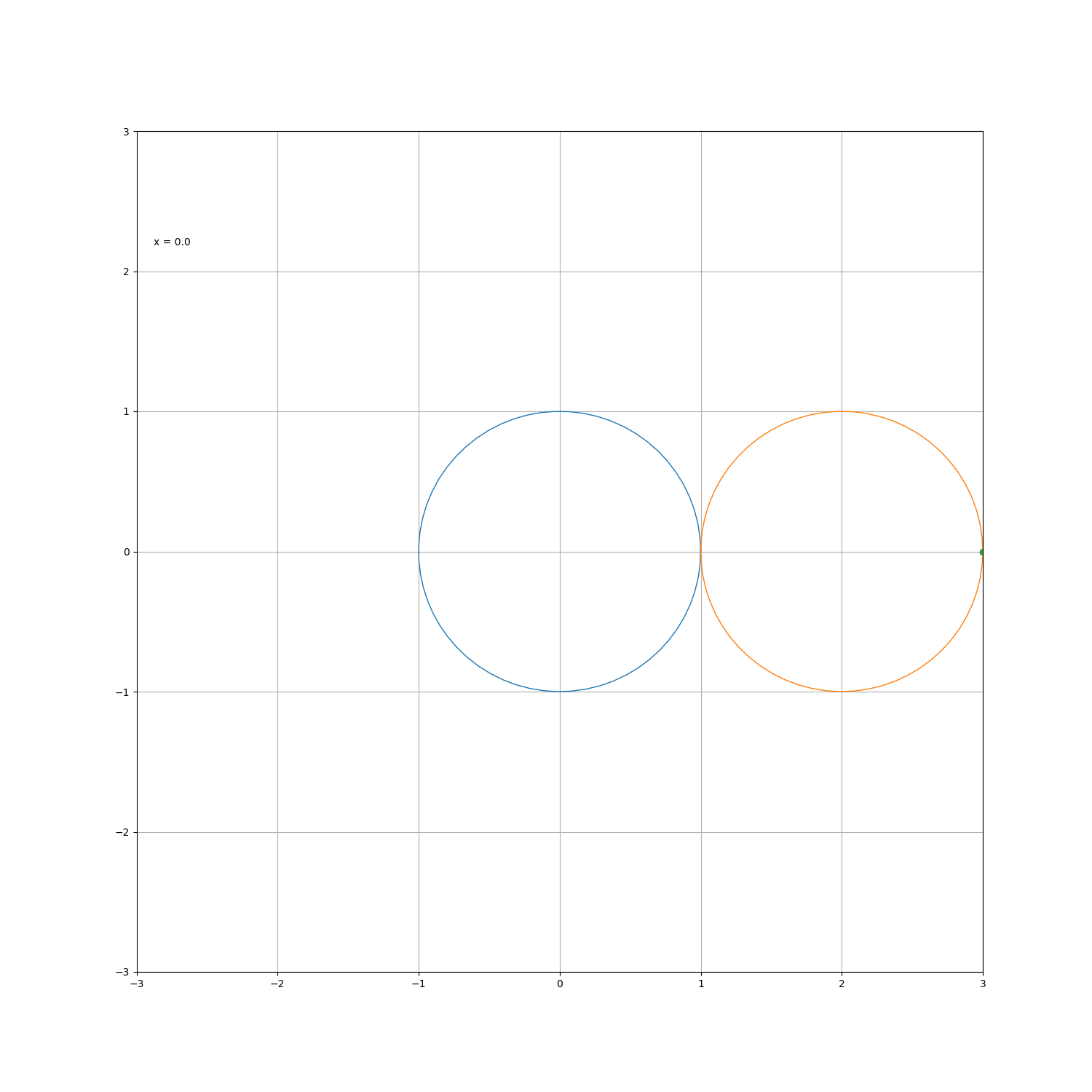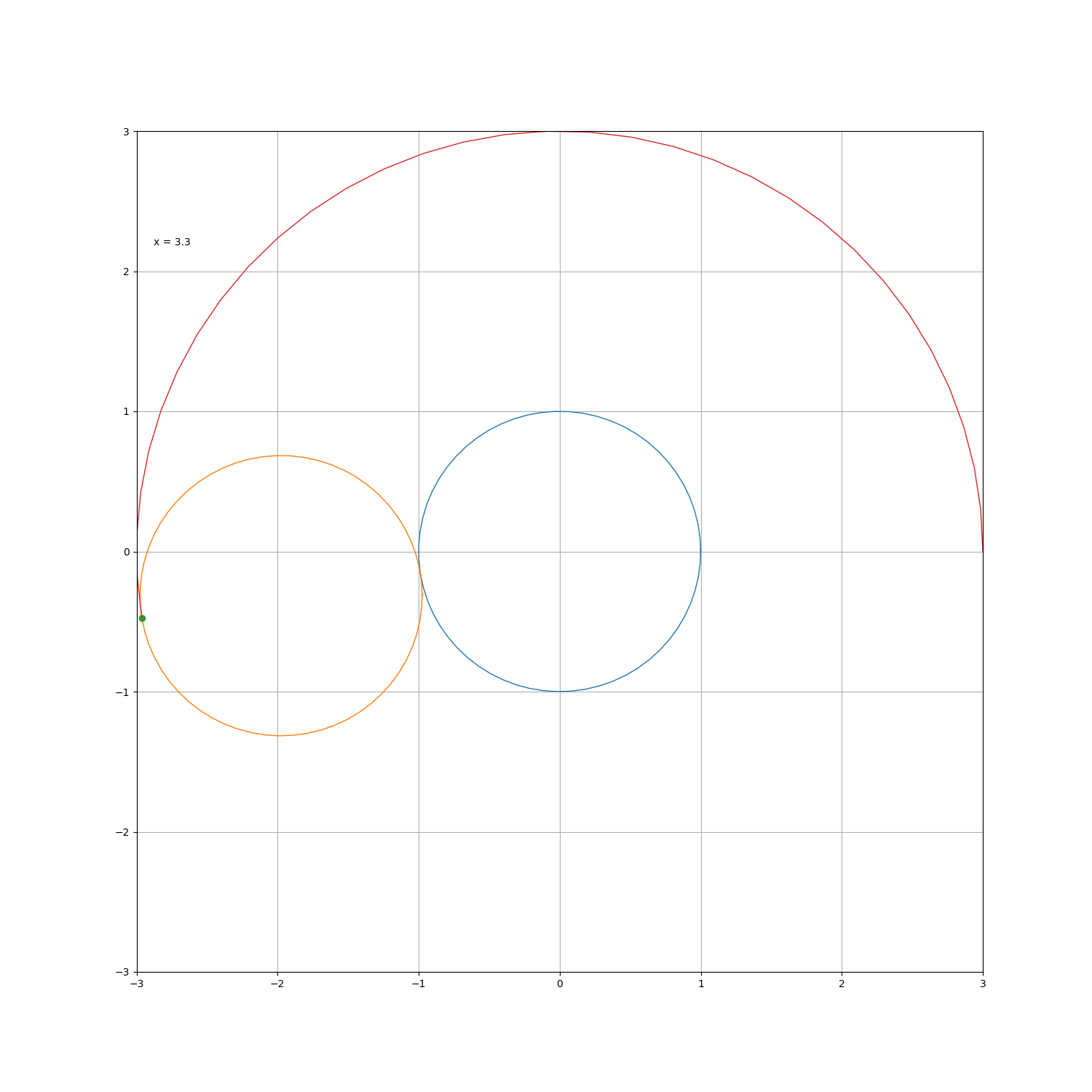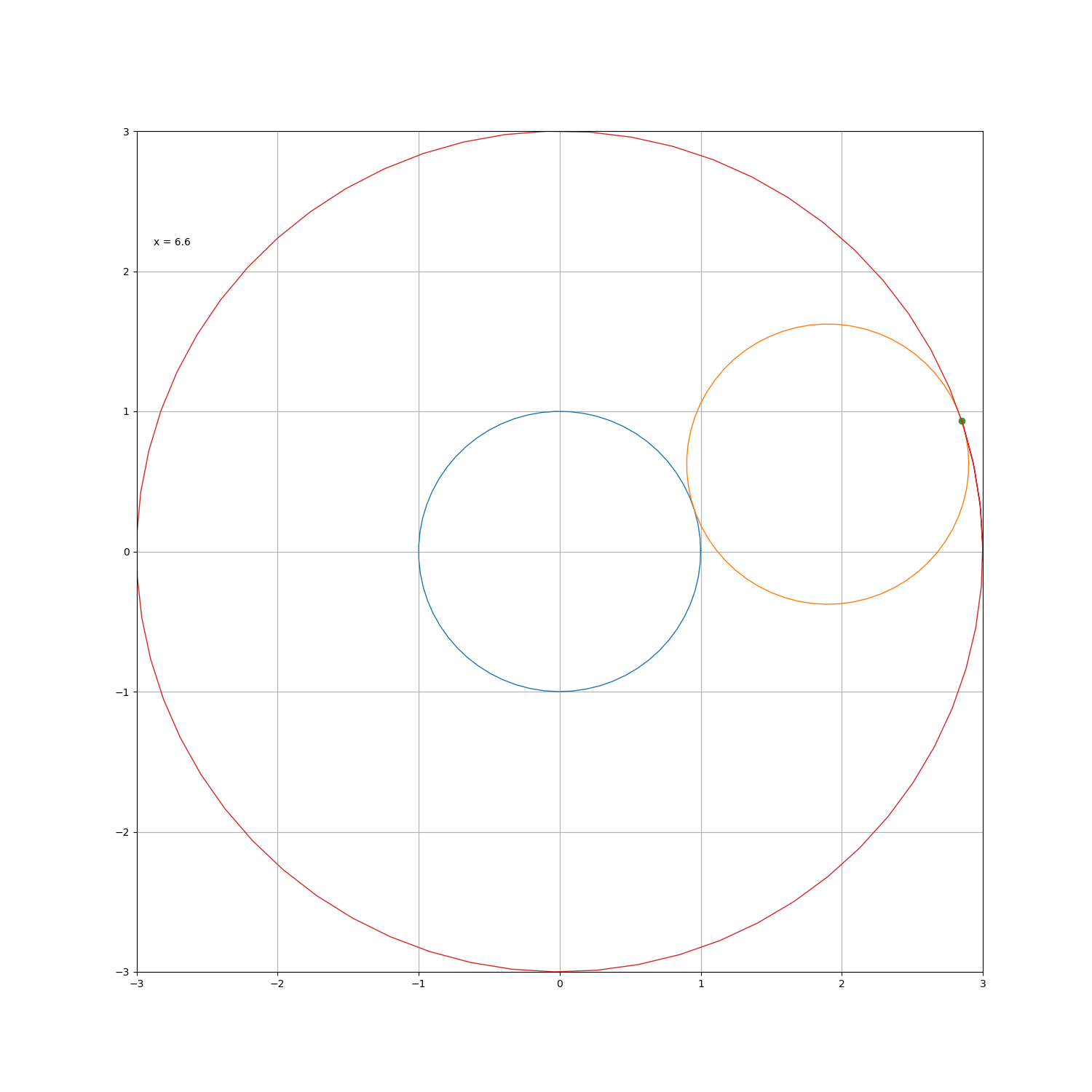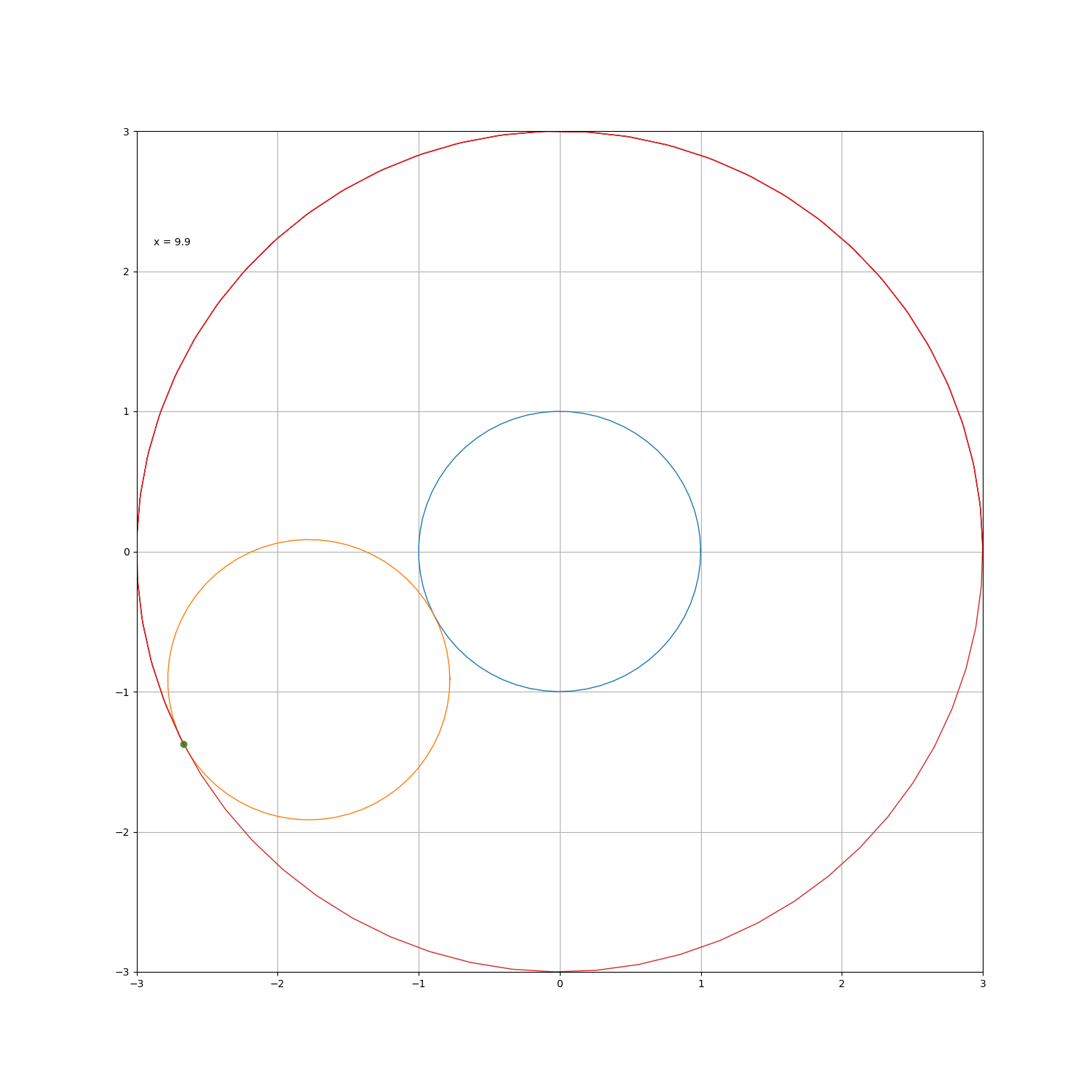
在这里插入图片描述

在这里插入图片描述

若选点 ( a , 0 ) 作为起点，则外摆线的参数方程为

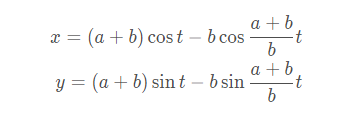
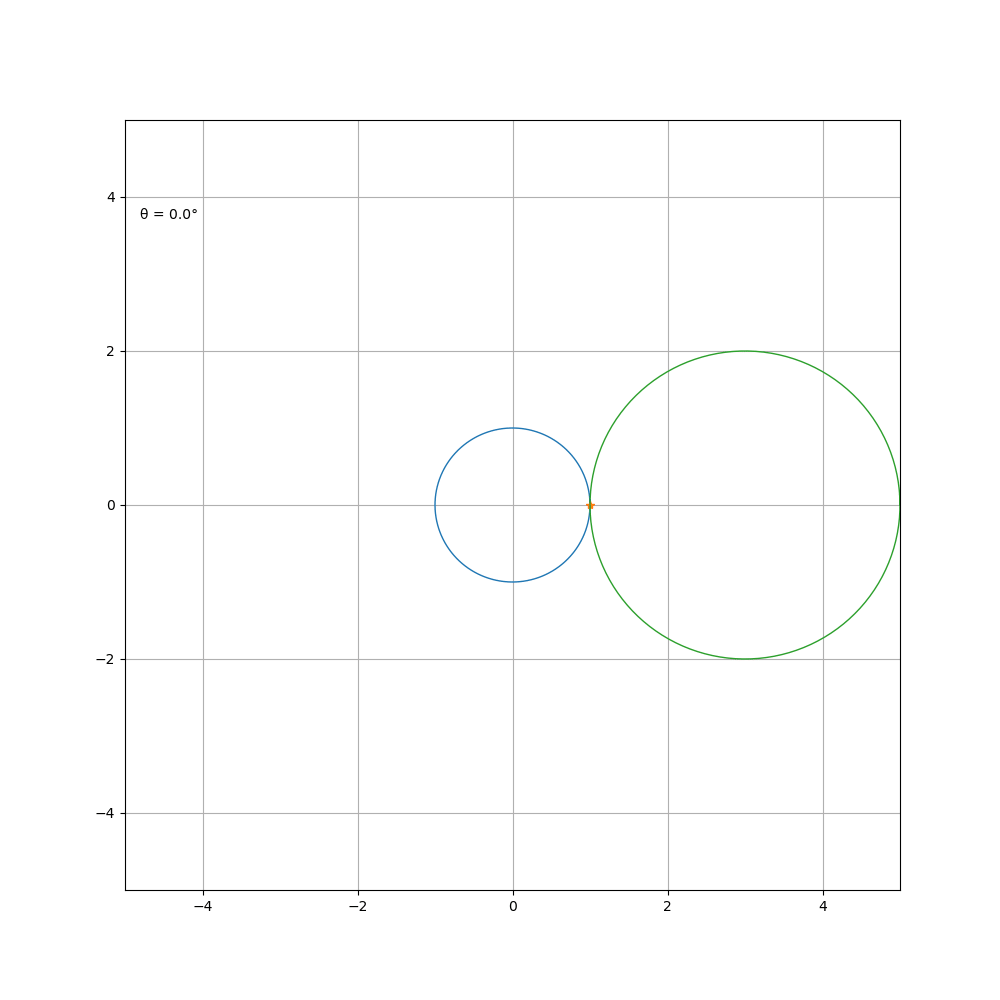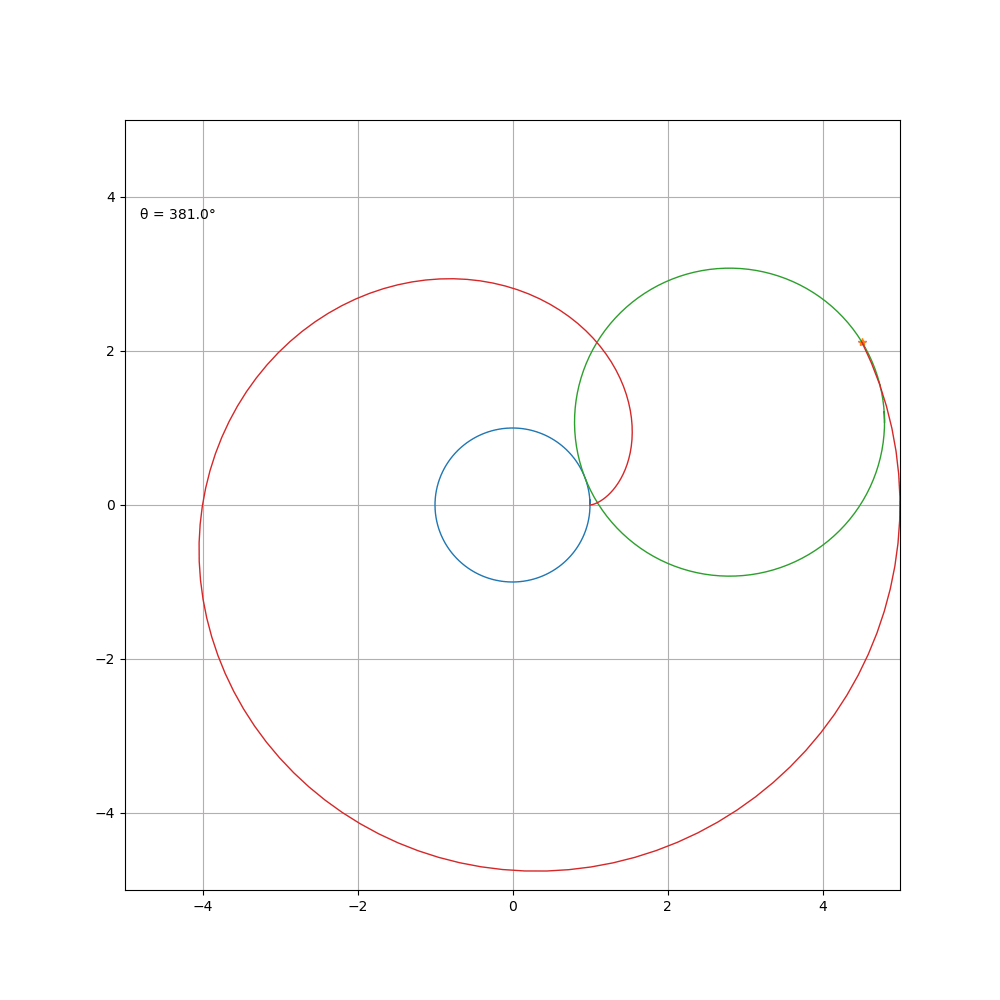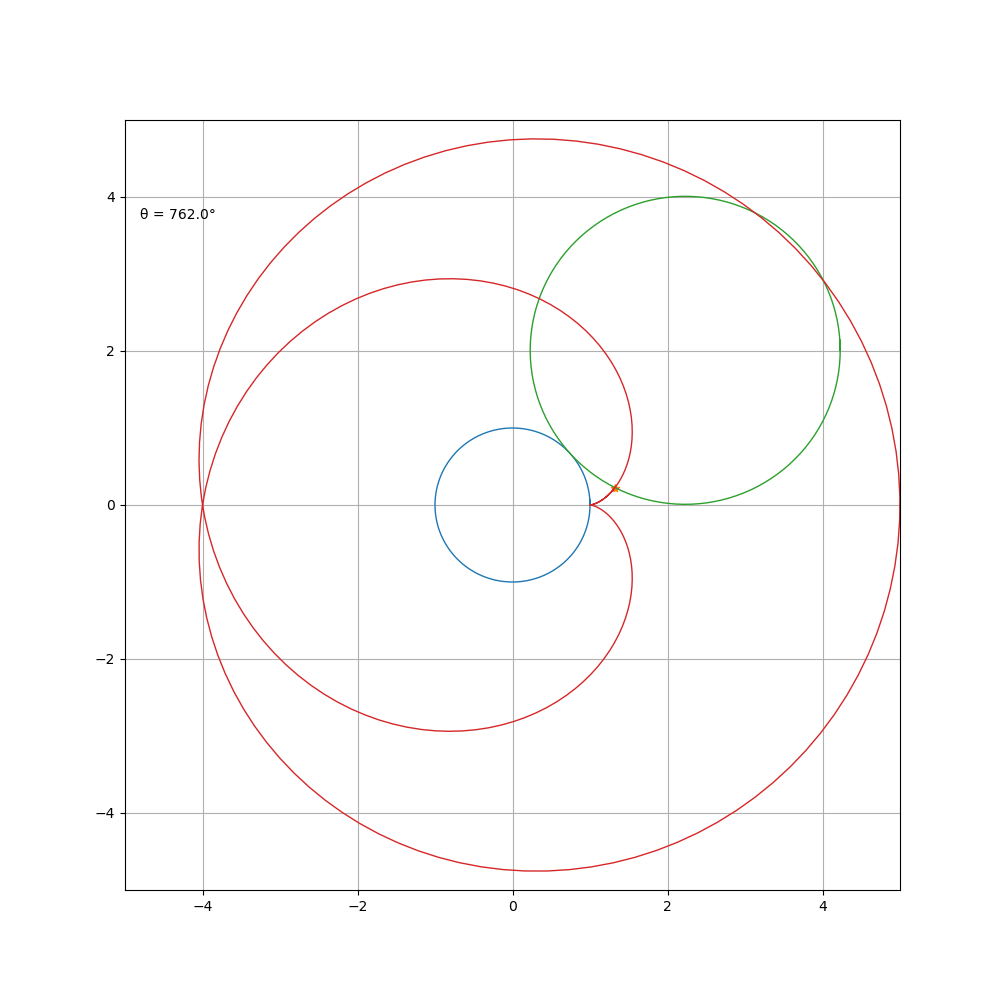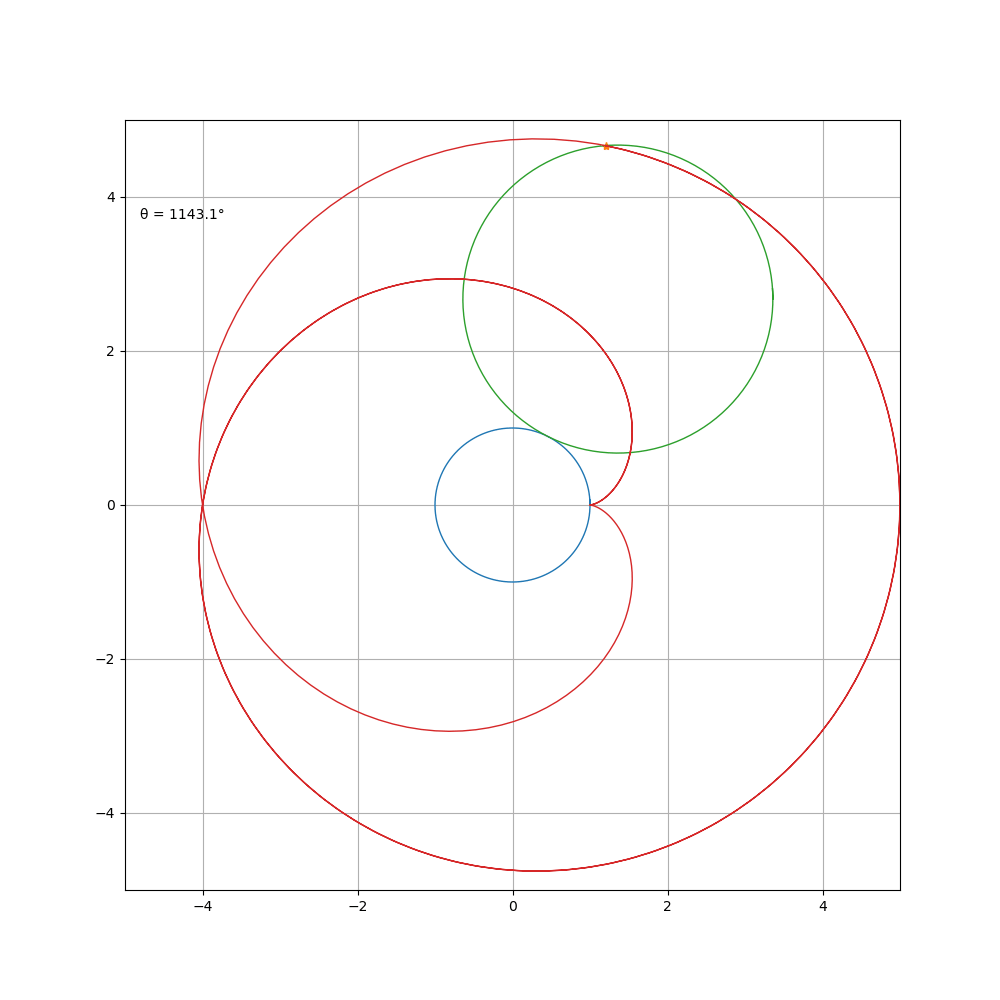
在这里插入图片描述

a = b 时就得到了著名的心脏线，被许多直男奉为经典

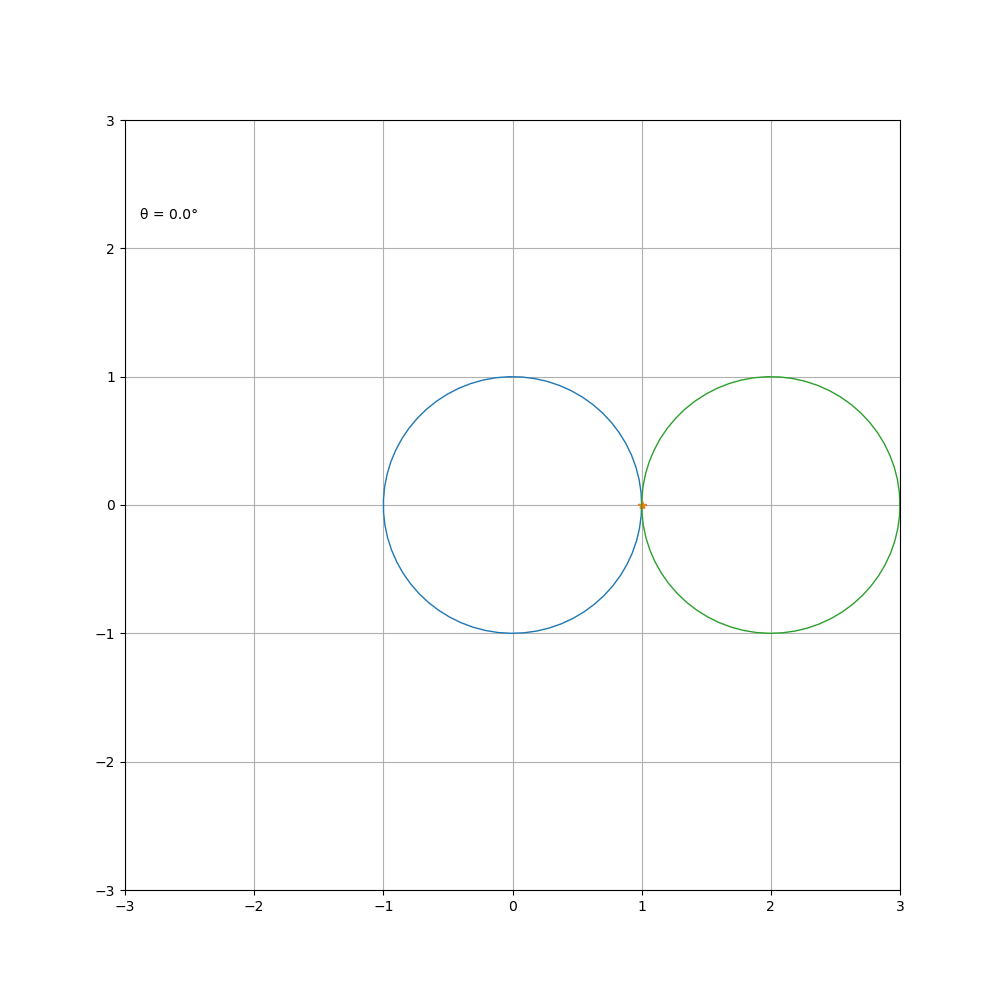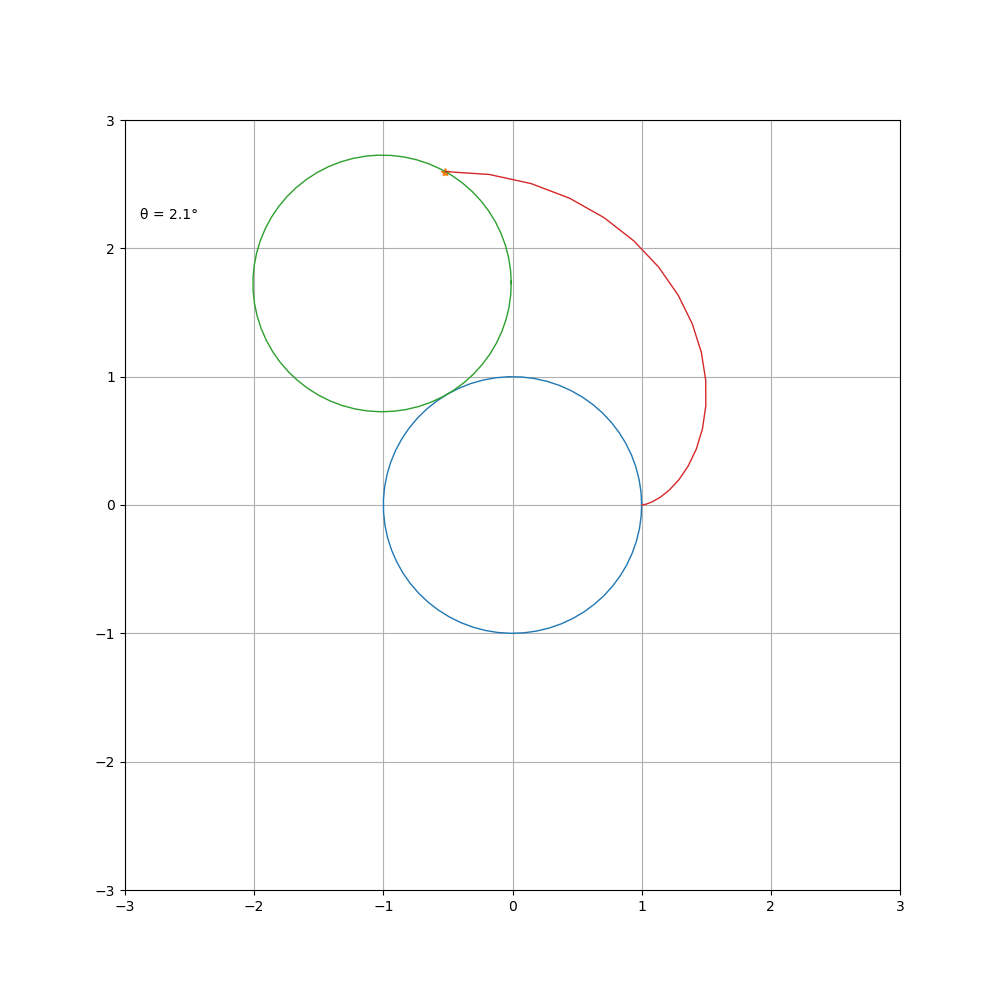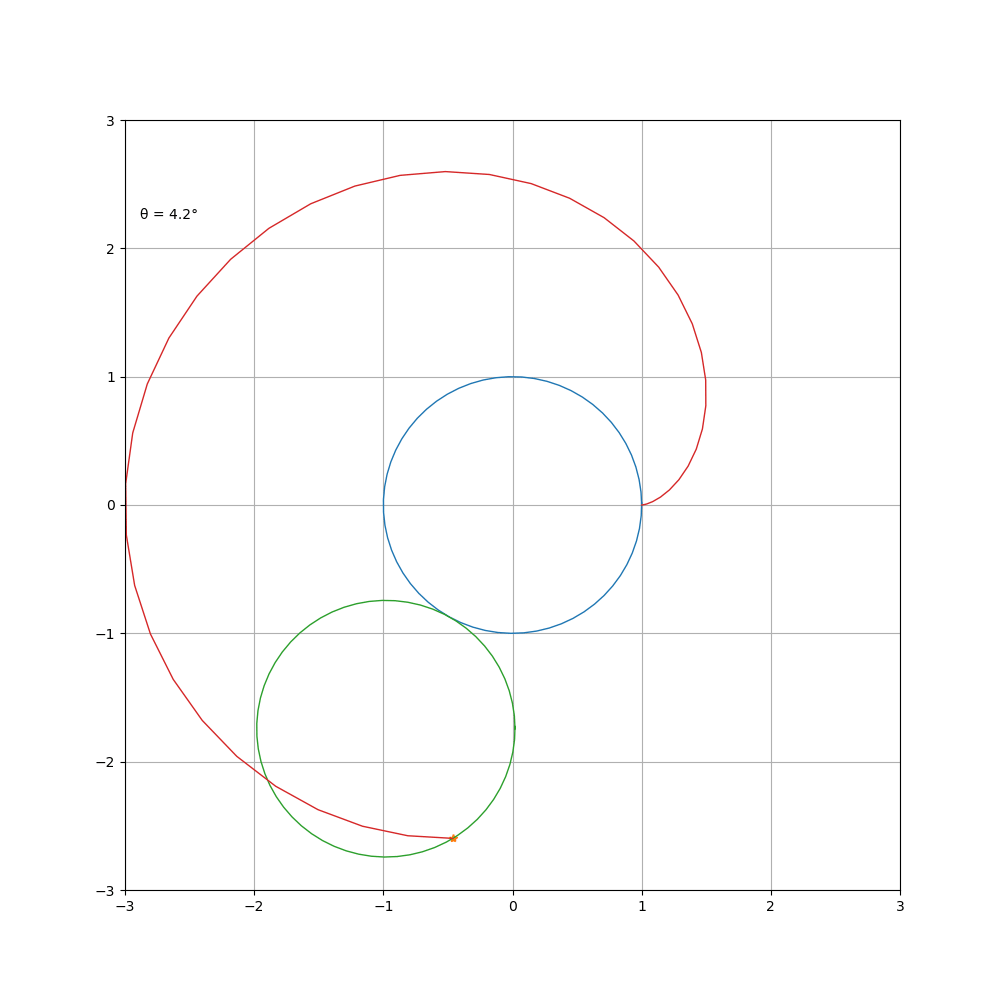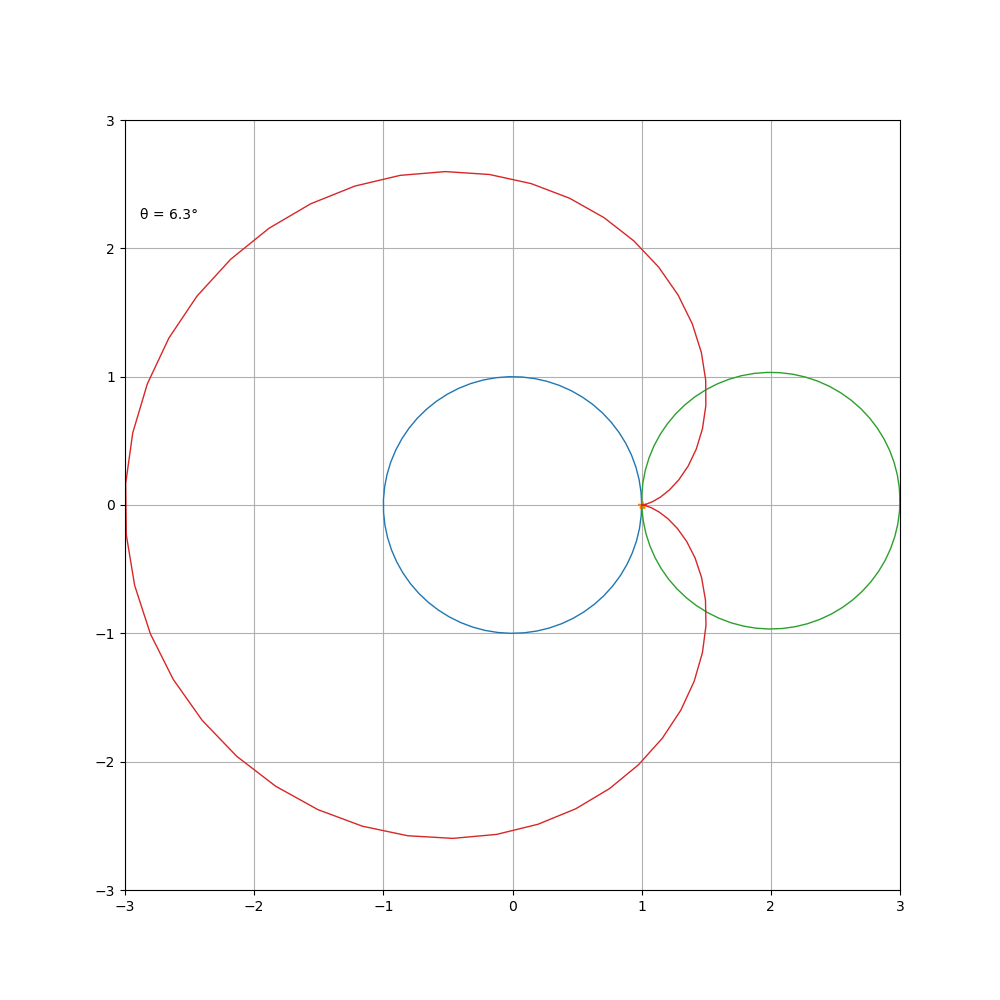
在这里插入图片描述

a = 1
b = 1
theta = np.arange(0,6.4,0.05)
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(autoscale_on=False, 
    xlim=(-3,3),ylim=(-3,3))
theta_text = ax.text(0.02,0.85,'',transform=ax.transAxes)
textTemplate = '''θ = %.1f°\n'''
ax.grid()
xCircle,yCircle = np.cos(theta),np.sin(theta)
ax.plot(a*xCircle,a*yCircle,'-',lw=1)
pt, = ax.plot([a+b],[0],'*')
cir, = ax.plot(a+b+b*yCircle,b*yCircle,'-',lw=1)
cycloid, = ax.plot([], [], '-', lw=1)
xs,ys = [],[]
def animate(t):
    if(t==0):
        xs.clear()
        ys.clear()    
    cenX = (a+b)*np.cos(t)
    cenY = (a+b)*np.sin(t)
    cir.set_data(cenX+b*xCircle,cenY+b*yCircle)
    newX = cenX - b*np.cos((a+b)/b*t)
    newY = cenY - b*np.sin((a+b)/b*t)
    xs.append(newX)
    ys.append(newY)
    pt.set_data([newX],[newY])
    cycloid.set_data(xs,ys)
    theta_text.set_text(textTemplate % t)
    return cycloid, cir, pt, theta_text
ani = animation.FuncAnimation(fig, animate, theta, 
    interval=50, blit=True)
ani.save("Cycloid.gif")
plt.show()

如果更改 a \ b比值，则可得到

 a \ b=2

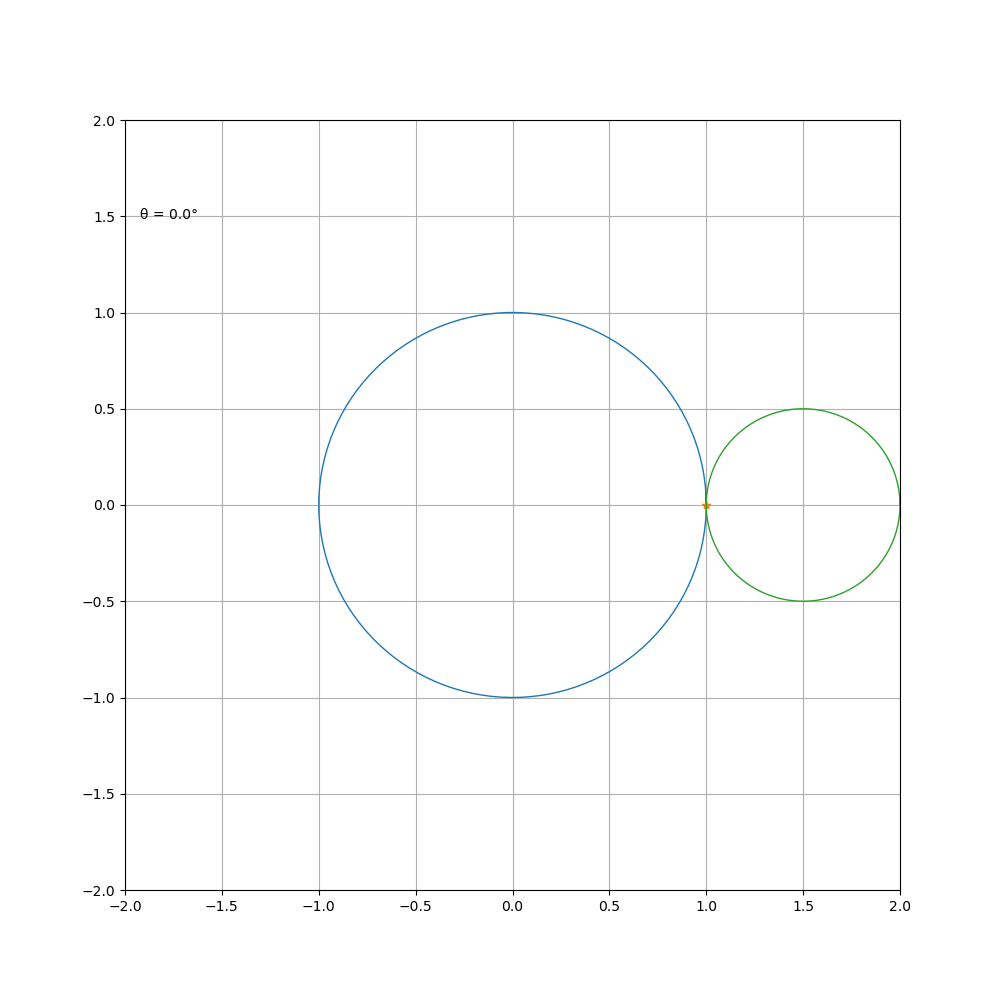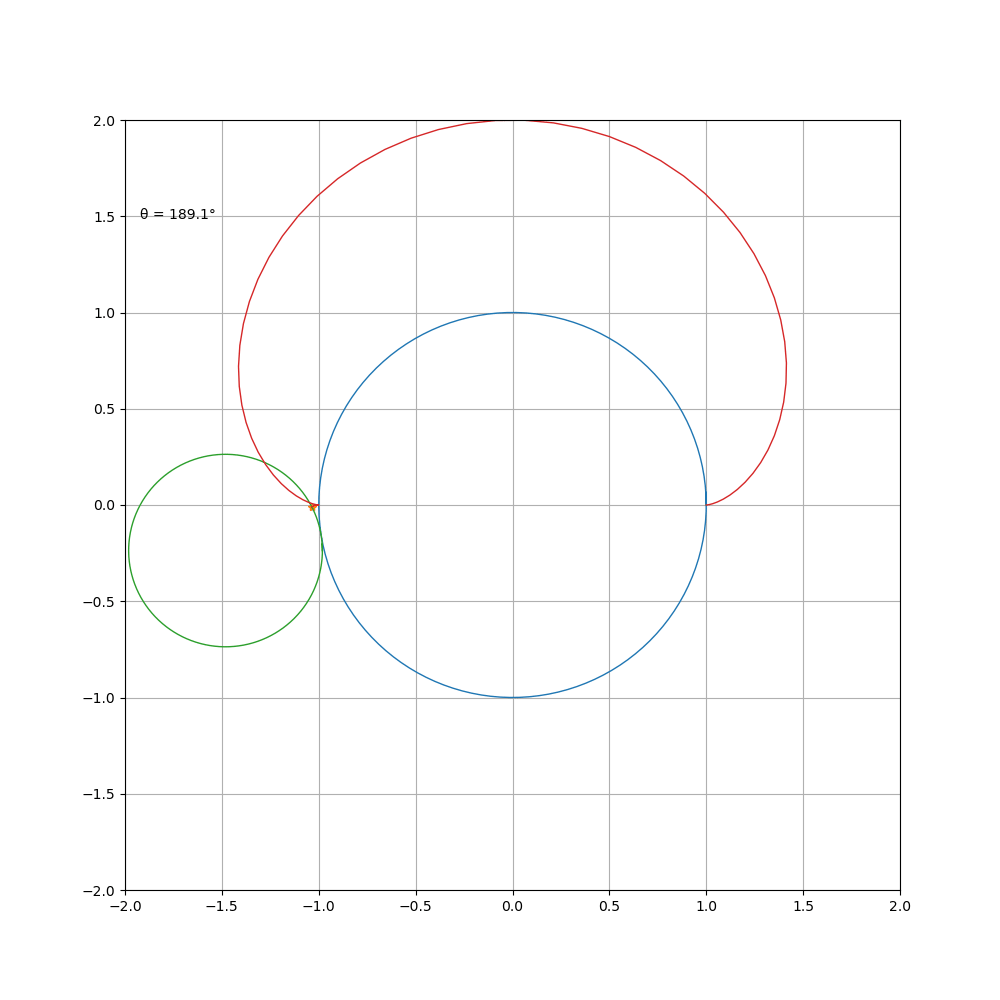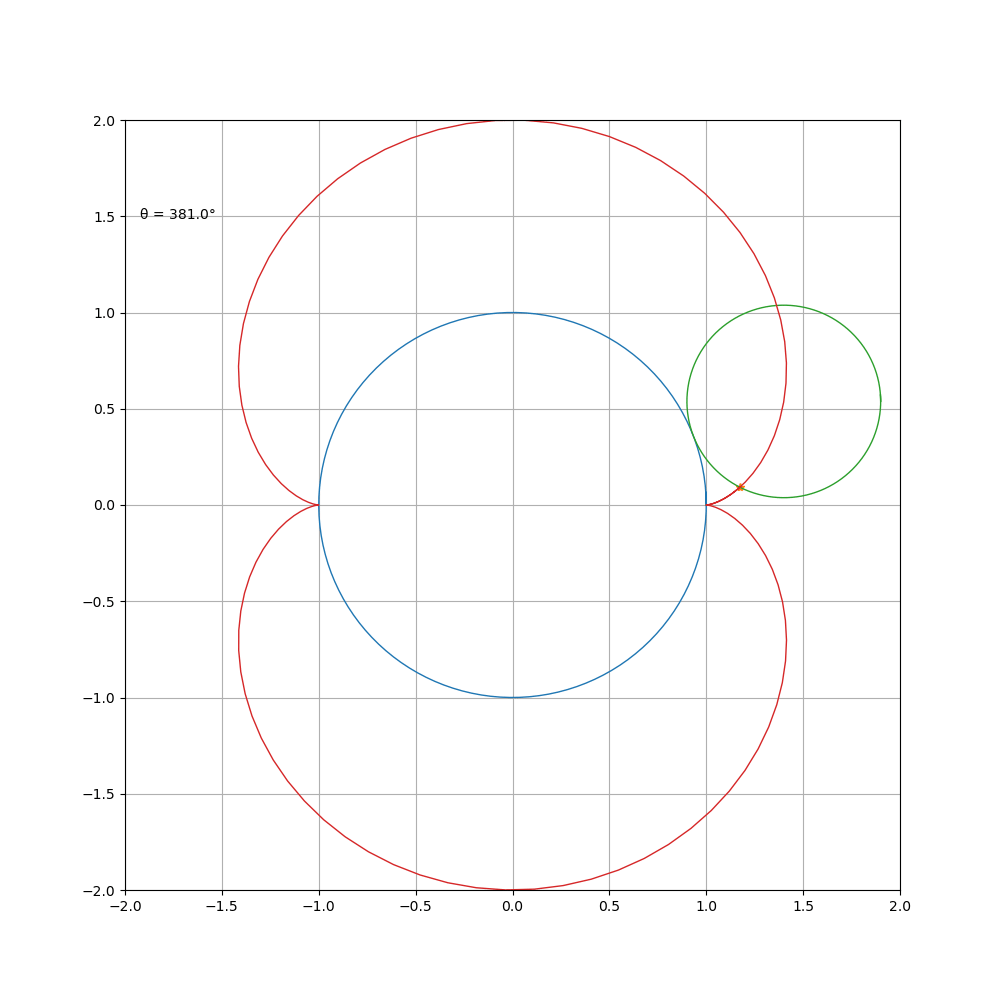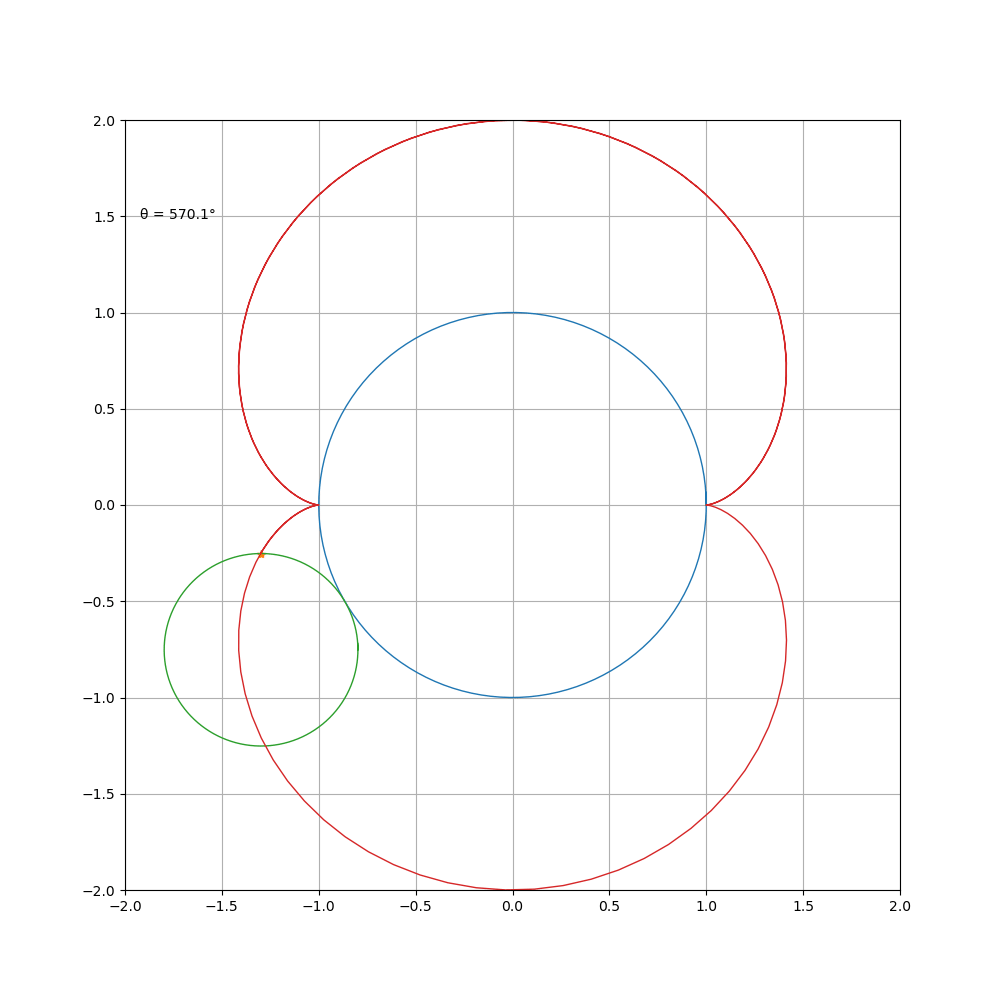
在这里插入图片描述 

 a \ b​=5

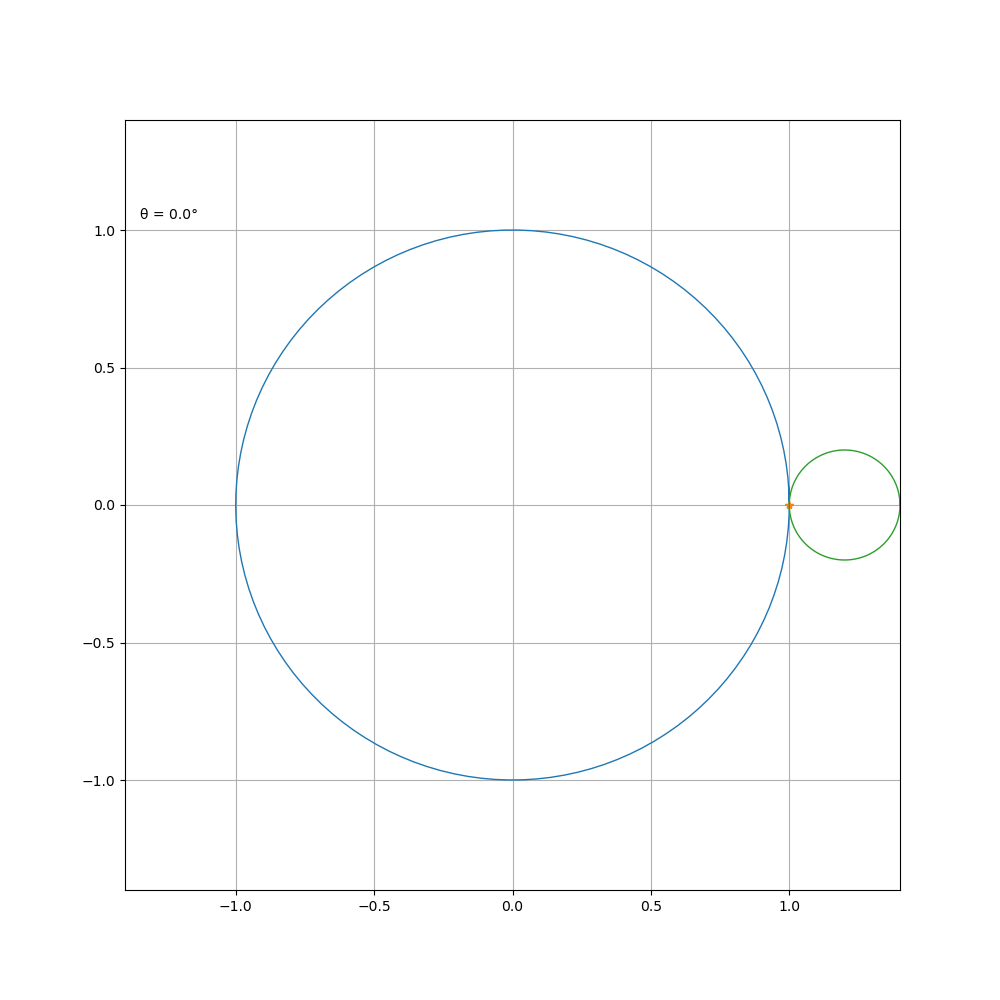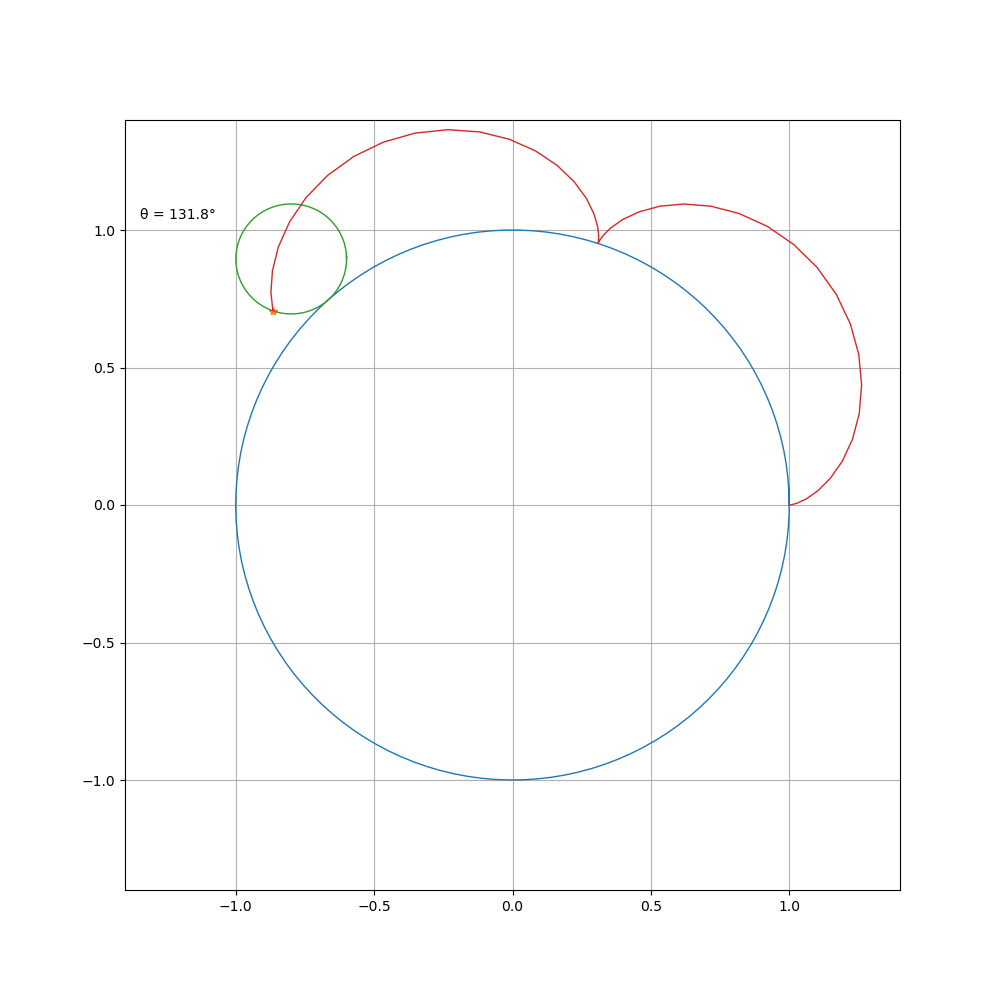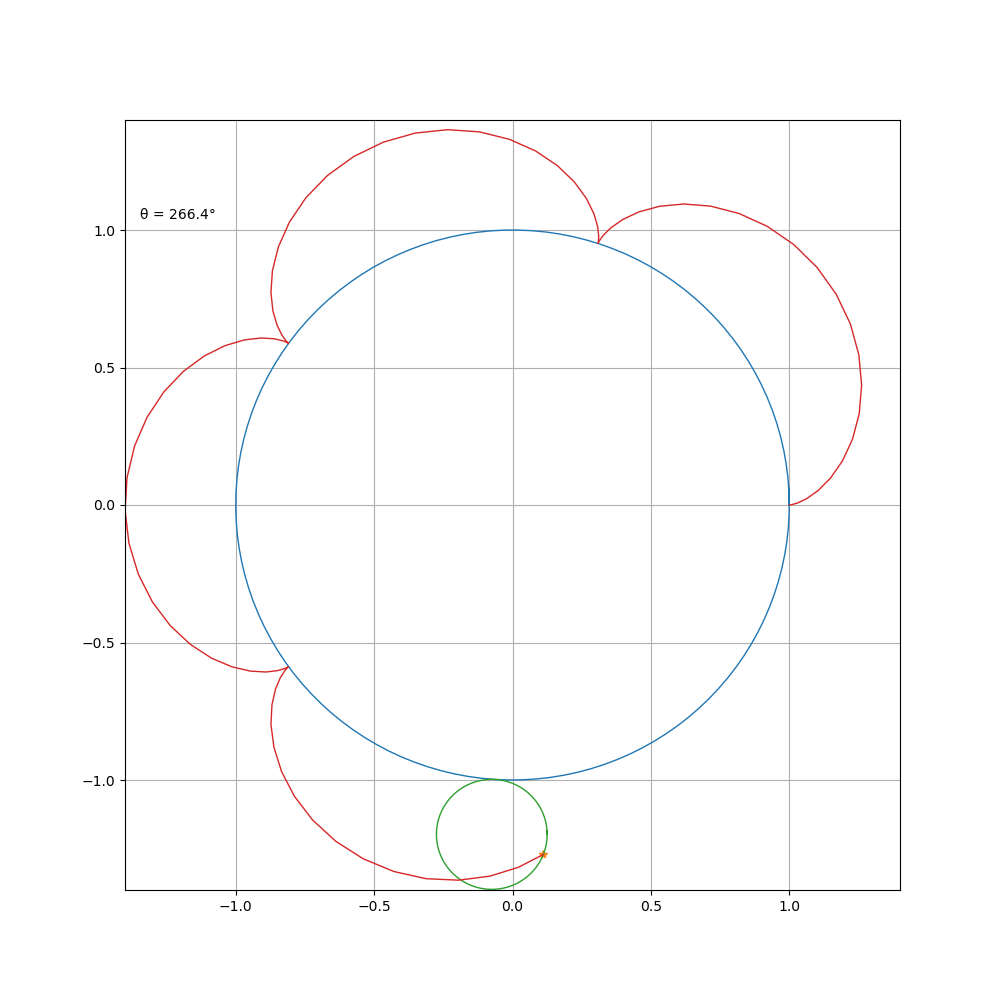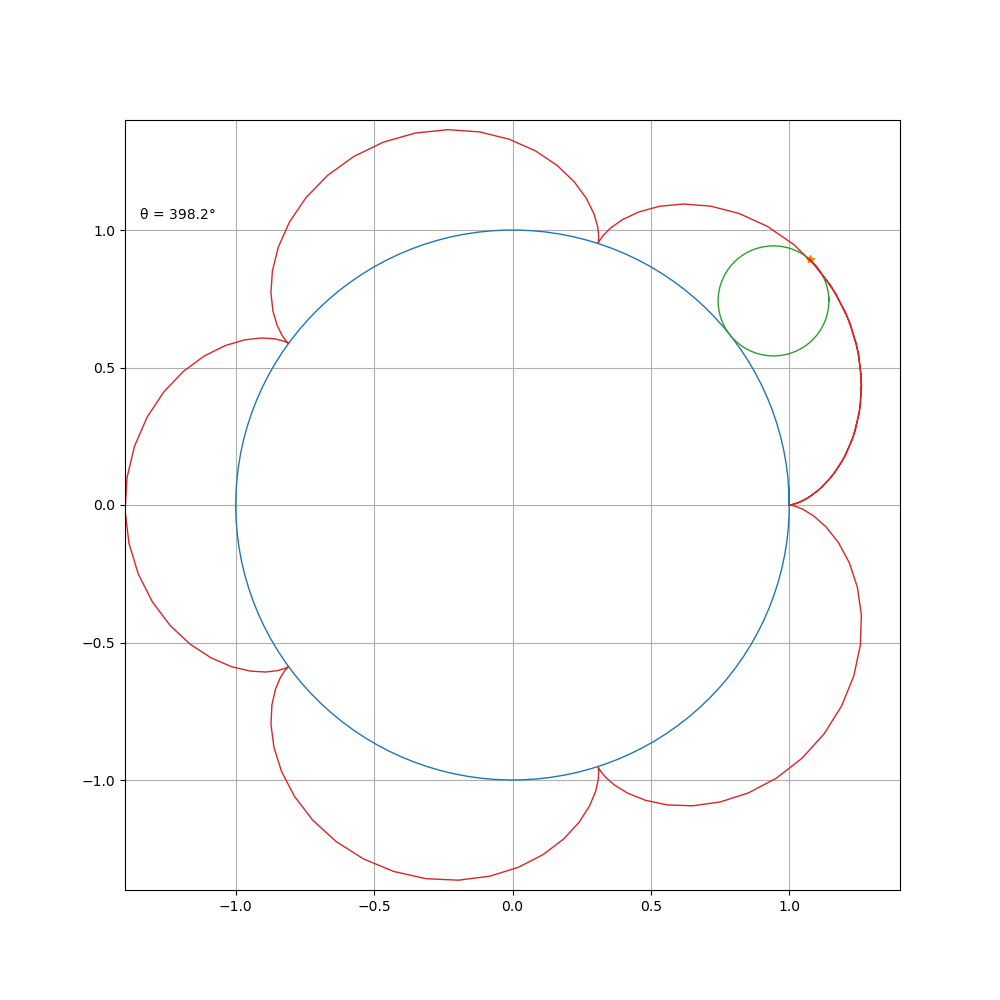
在这里插入图片描述 

 a \ b=1\2

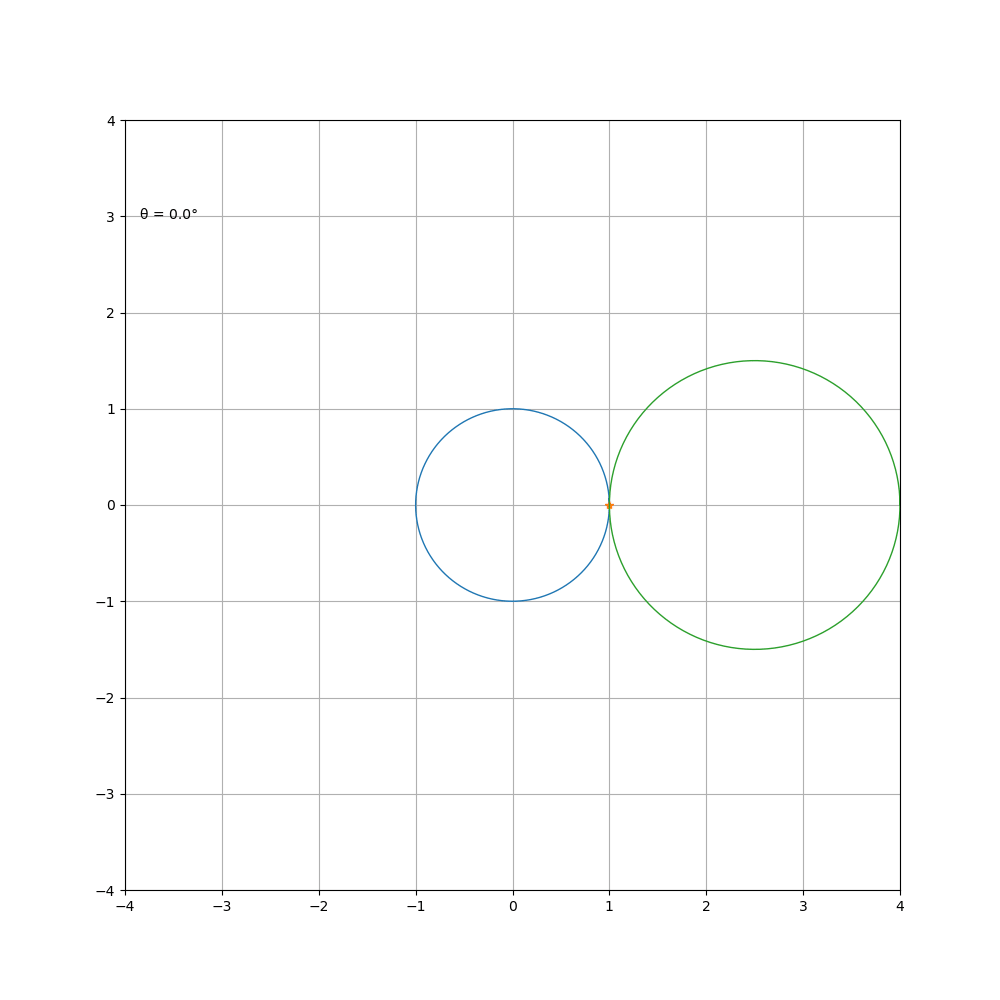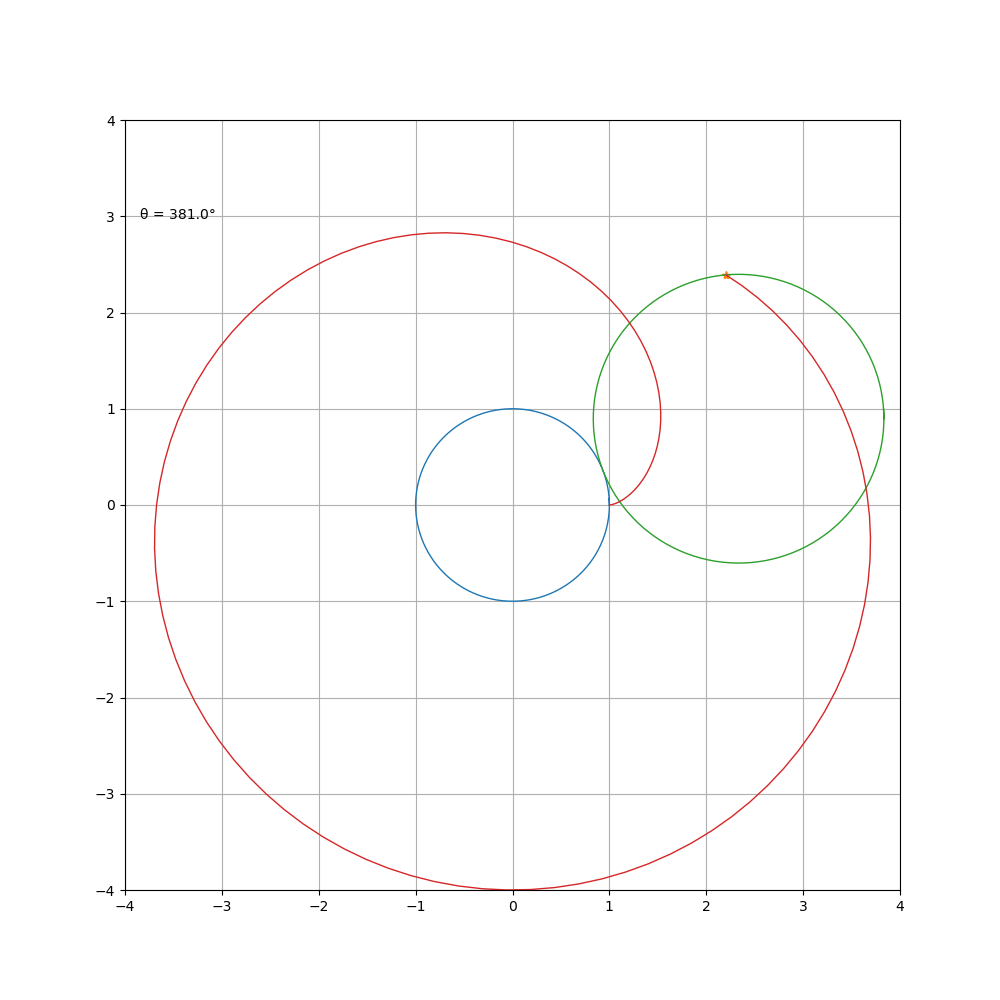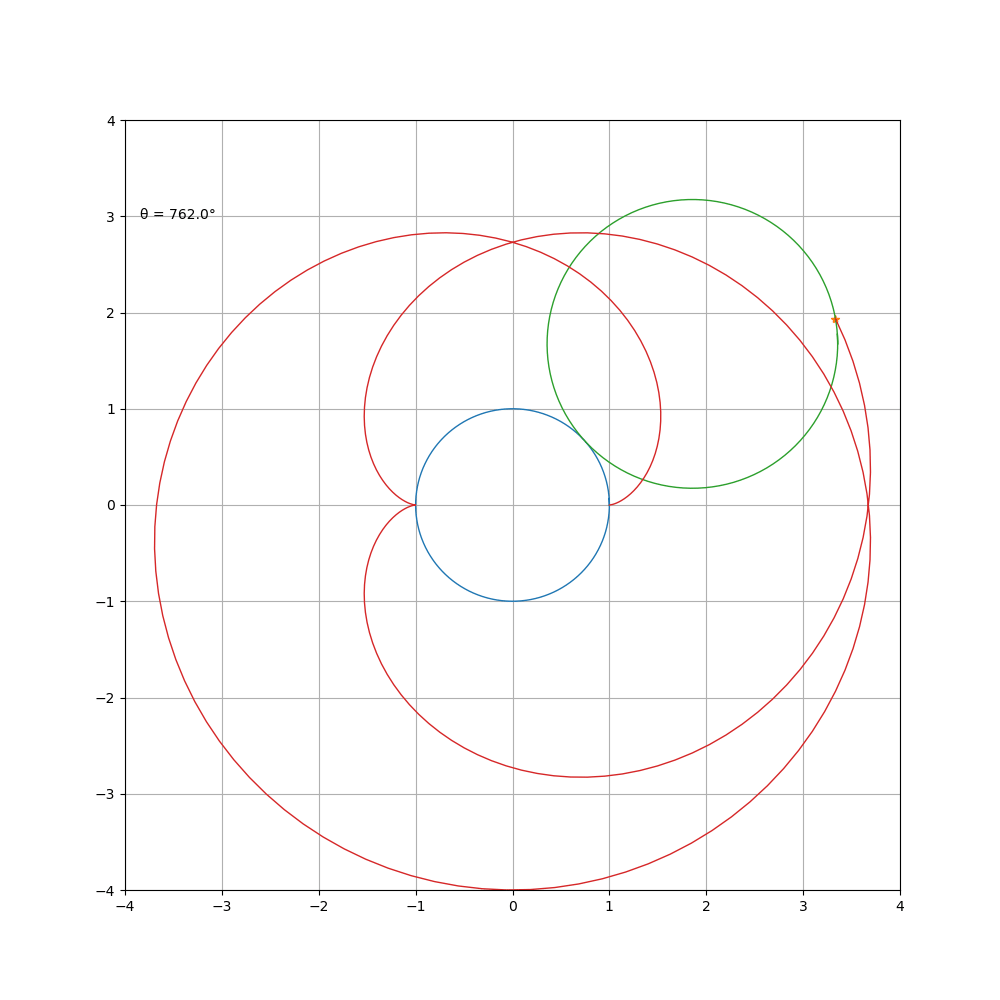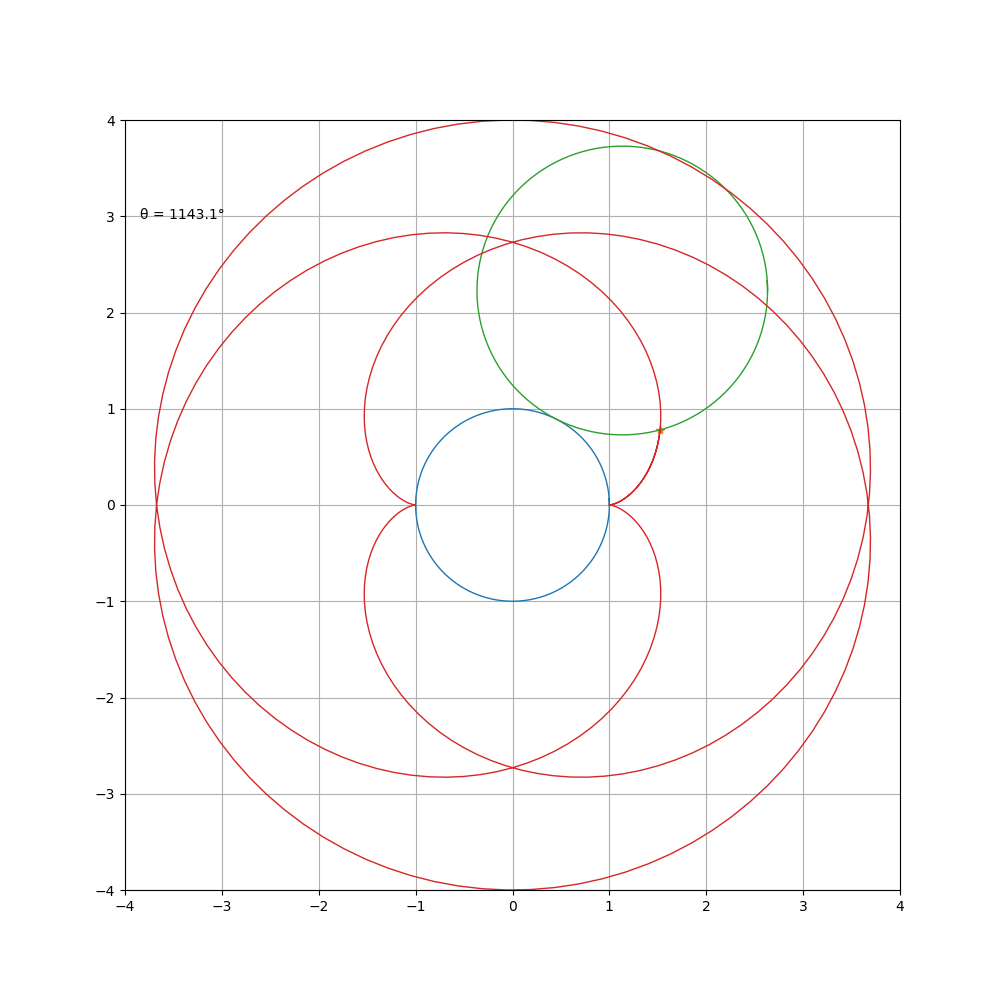
在这里插入图片描述

 a \ b​=2\3​

在这里插入图片描述

对 a\b进行约分得到 m \ n​，曲线由 m支组成，总共绕定圆 n周，然后闭合。观察 1 \b = 1 \2 时的曲线，可以看到其前 p i 个值和后 π 个值组成的心形更好看。

如果 a\b​是无理数，则永远也不会闭合，例如令 b = e ，由于图片超过5M，所以就不上传了。这个图总共转了17圈，到后期十分考验视力，为了让规律更清晰，我们选择只绘制尖点附近的运动状态，

在这里插入图片描述

内摆线与星形线

当动圆在定圆内部转动时，则为内摆线，其方程为

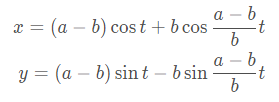
在这里插入图片描述

a\b​=2

在这里插入图片描述 

a\b​=4

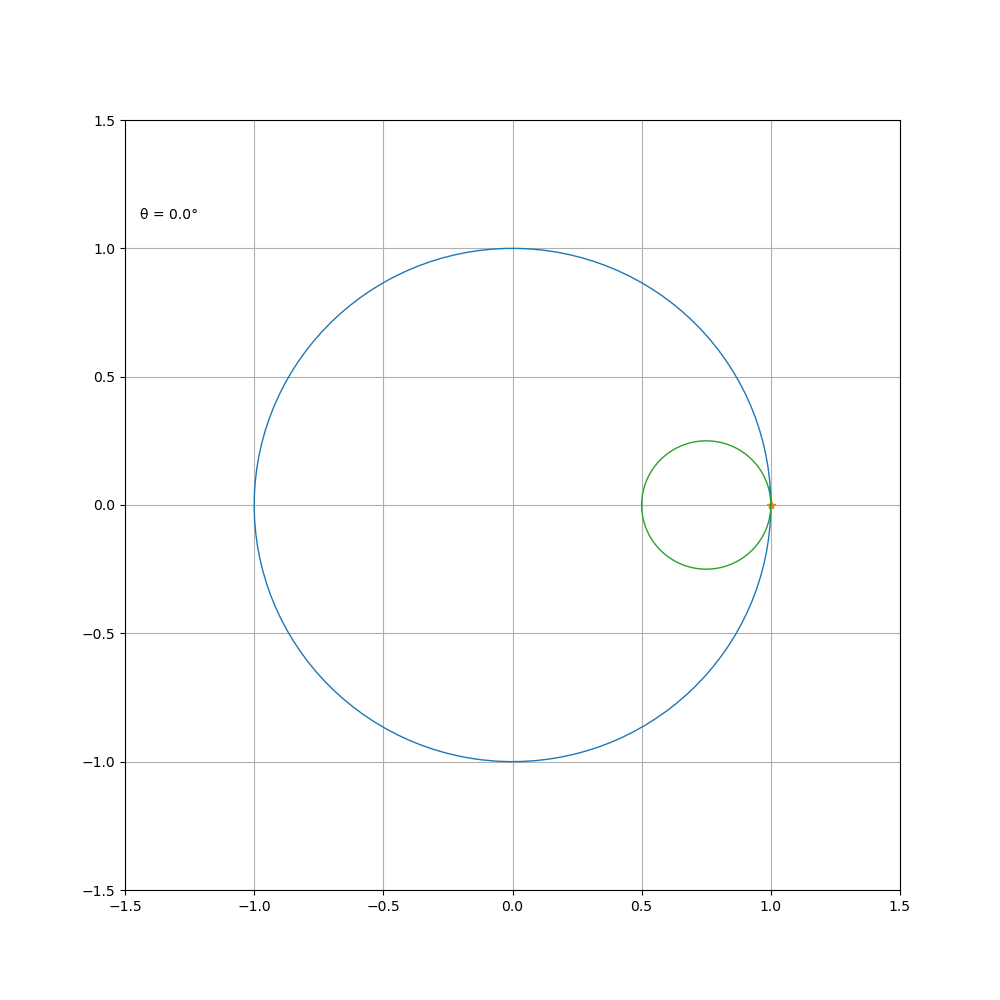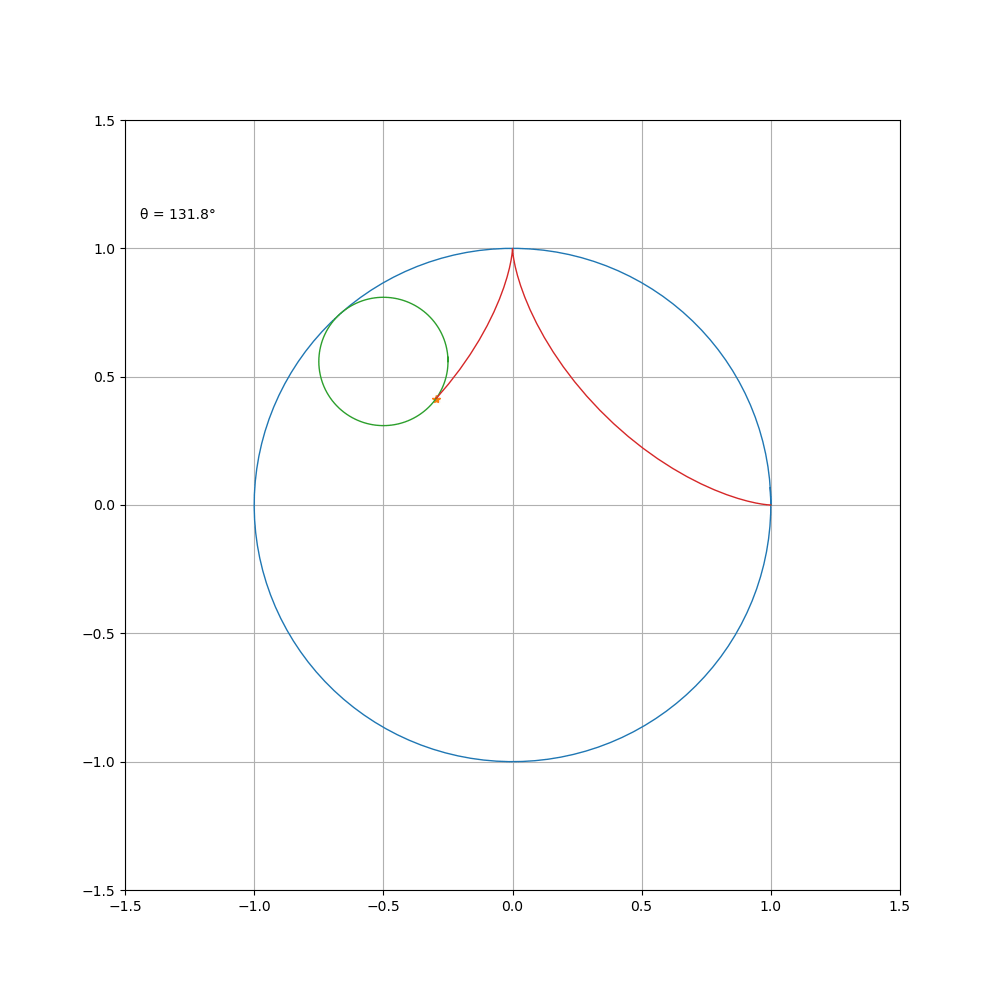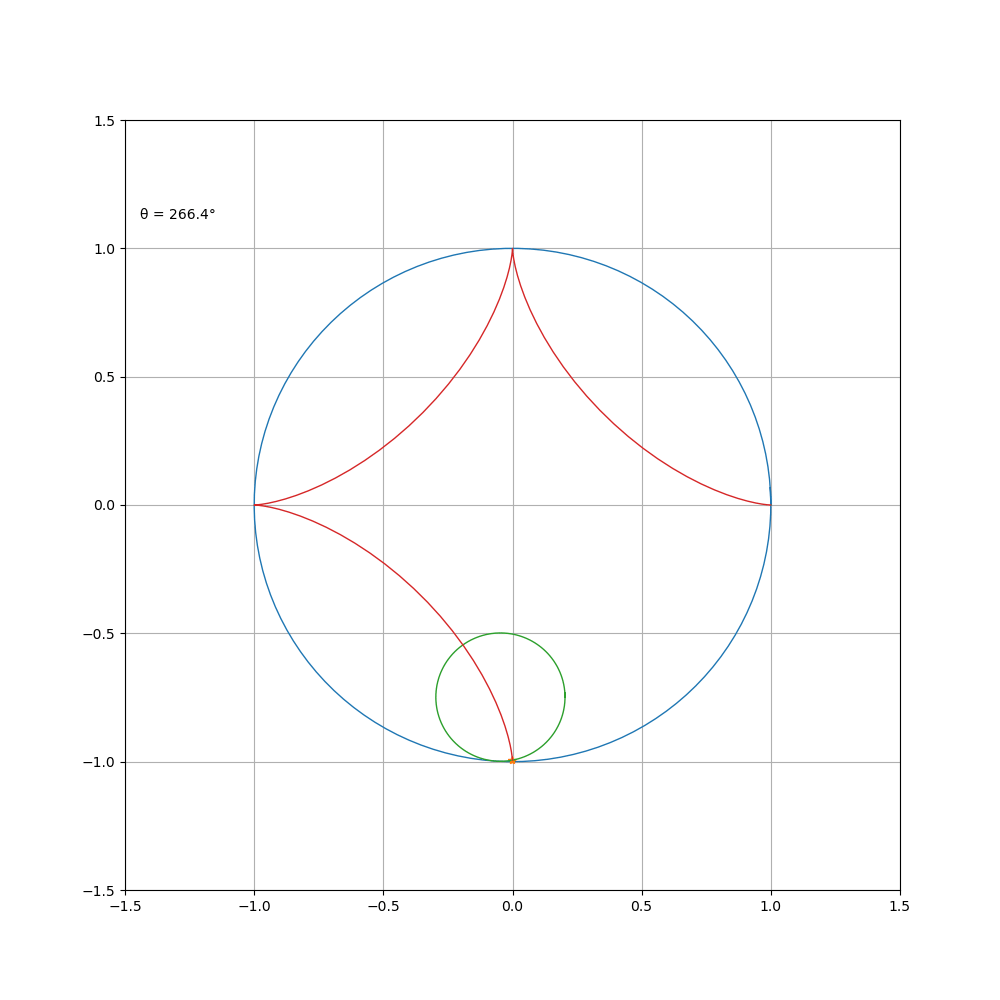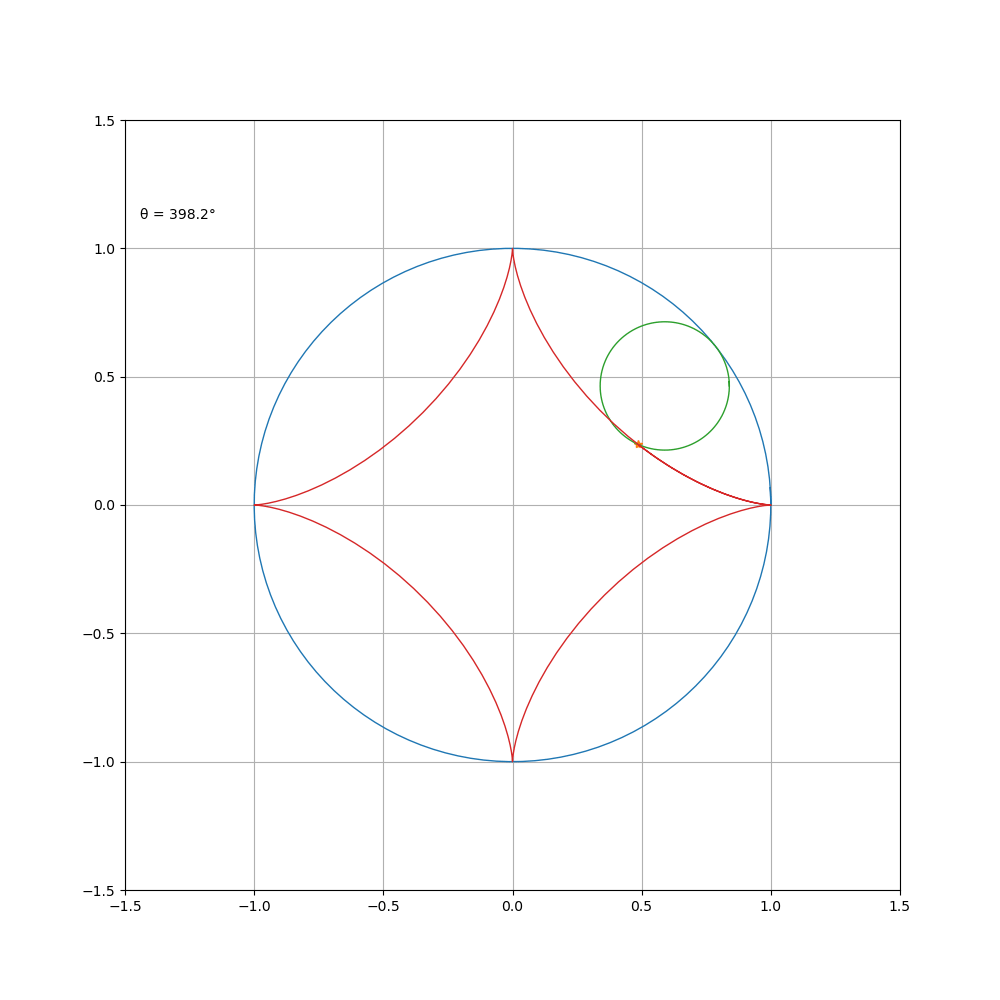
在这里插入图片描述 

a\b=5

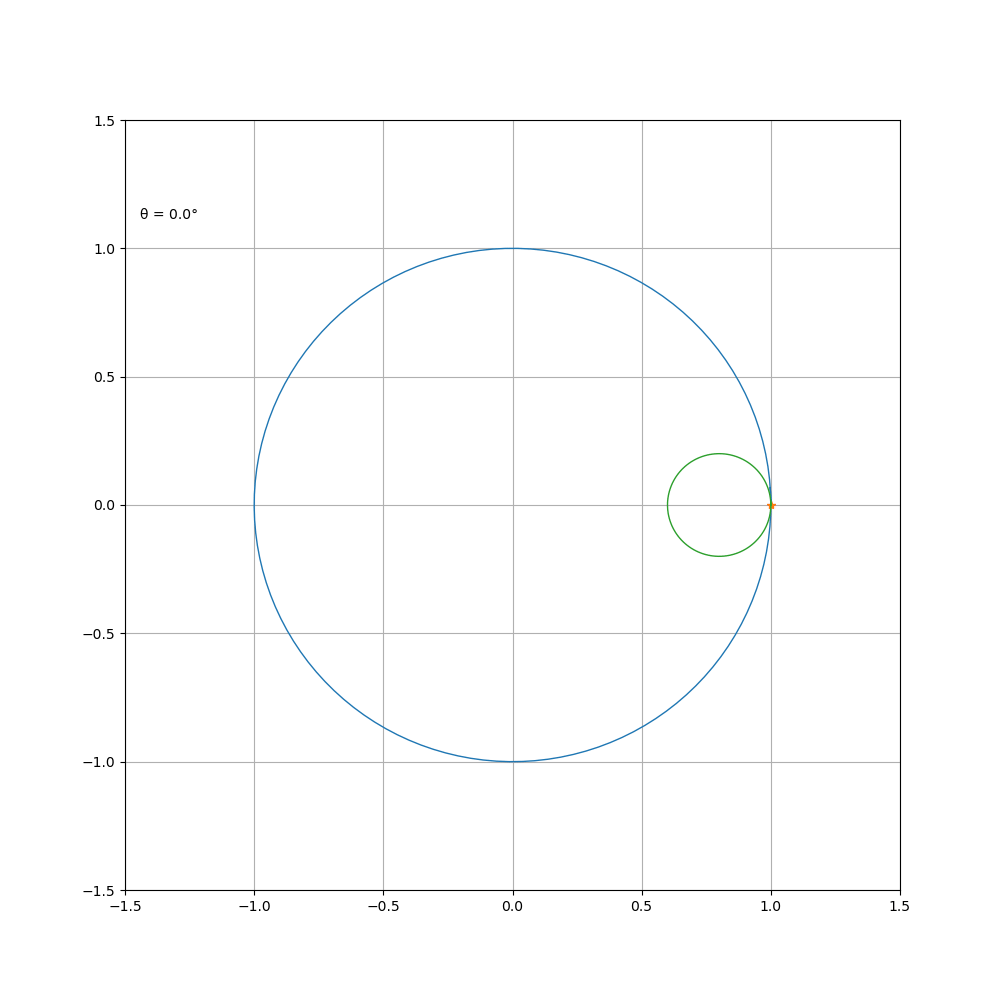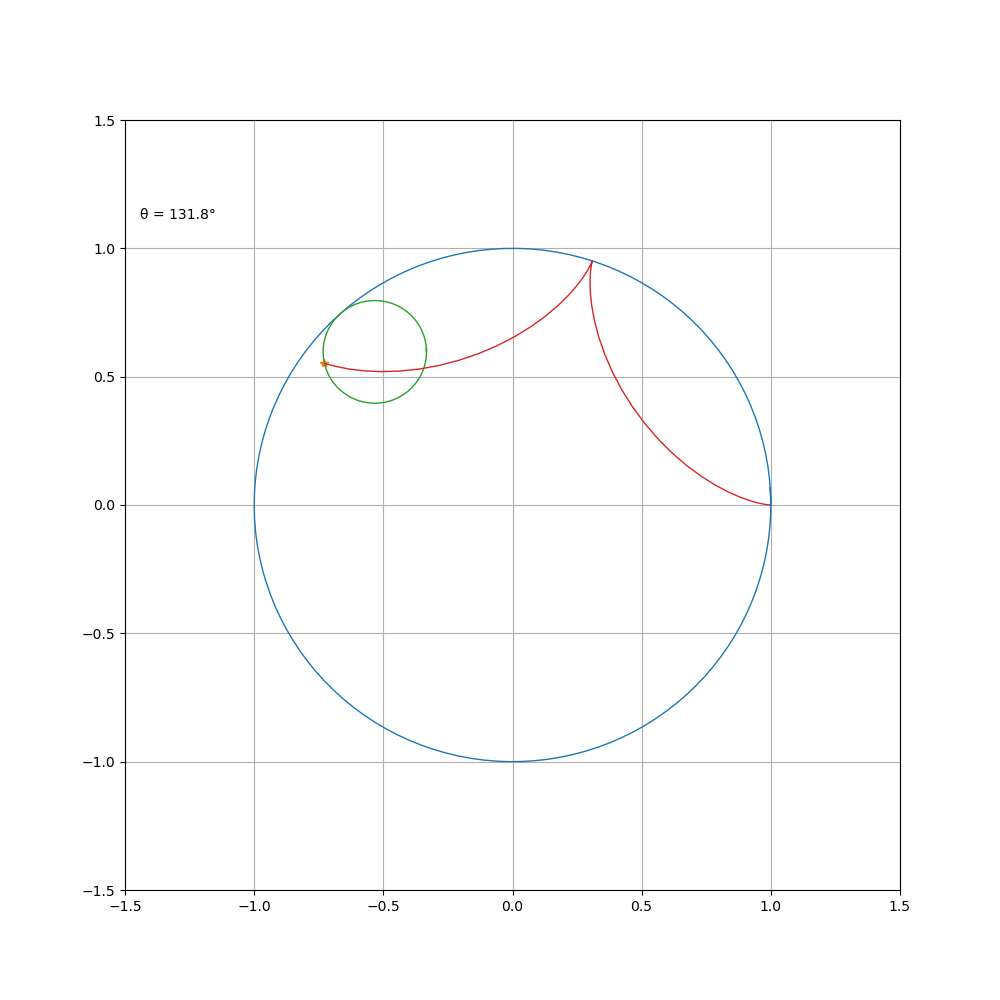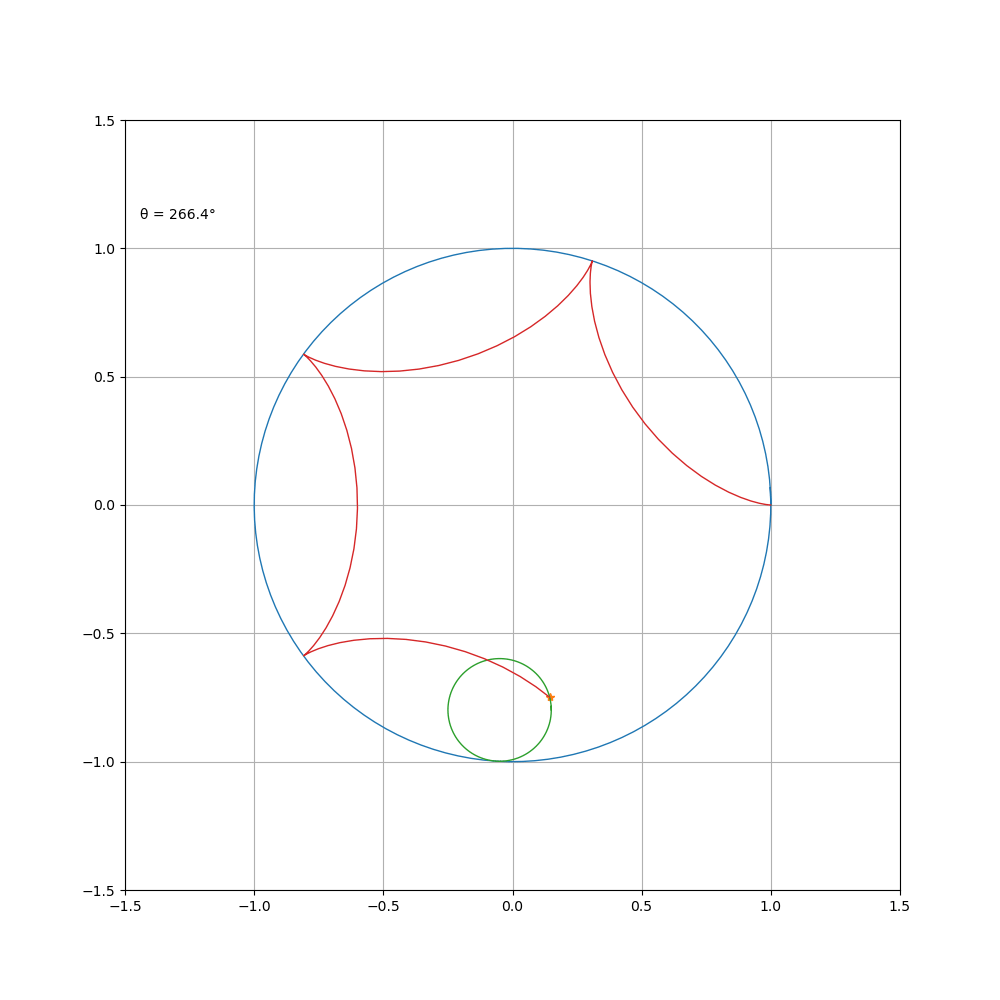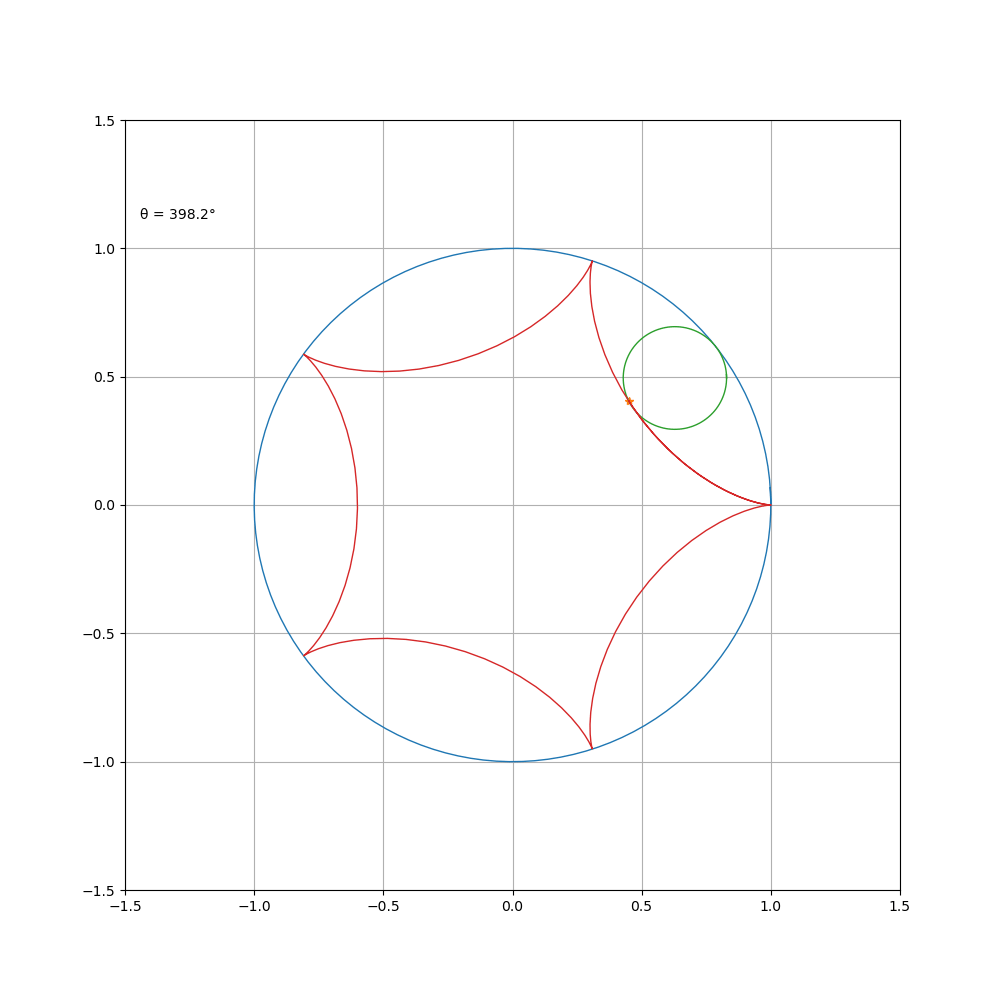
在这里插入图片描述 

a \b = 1\3

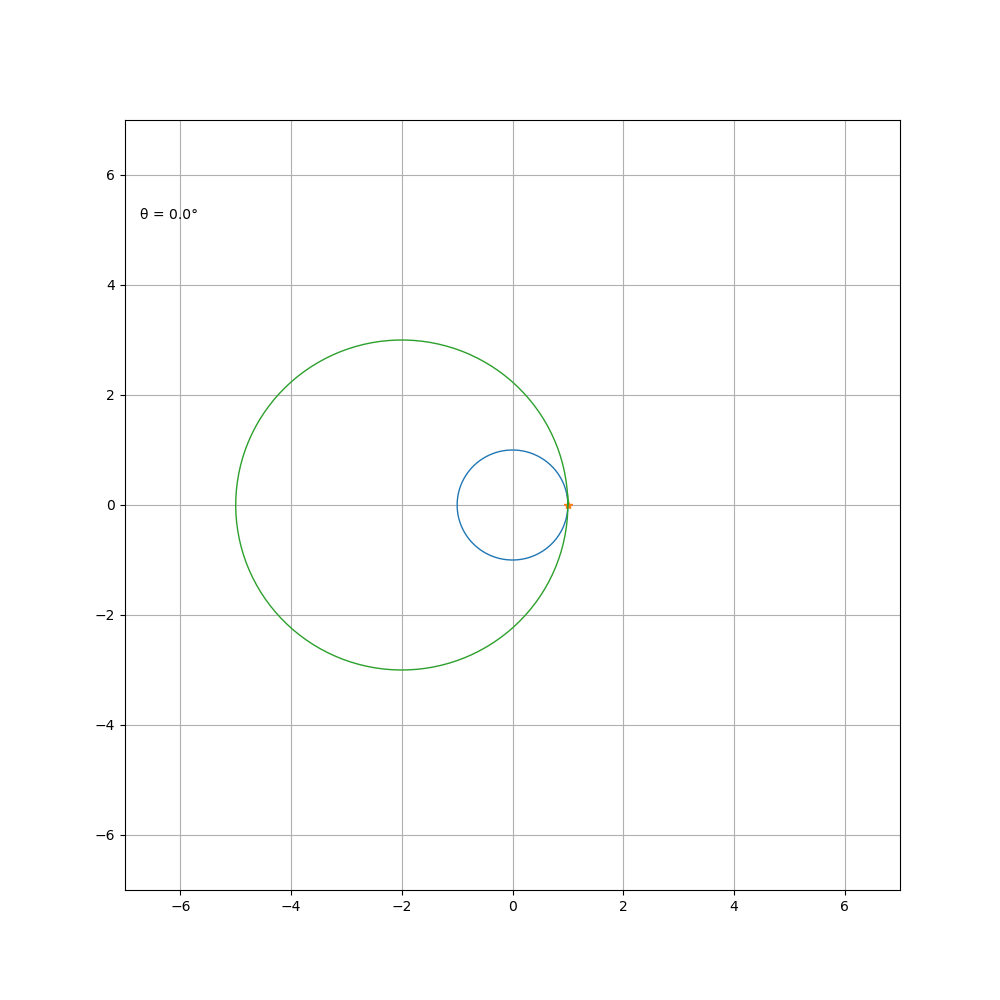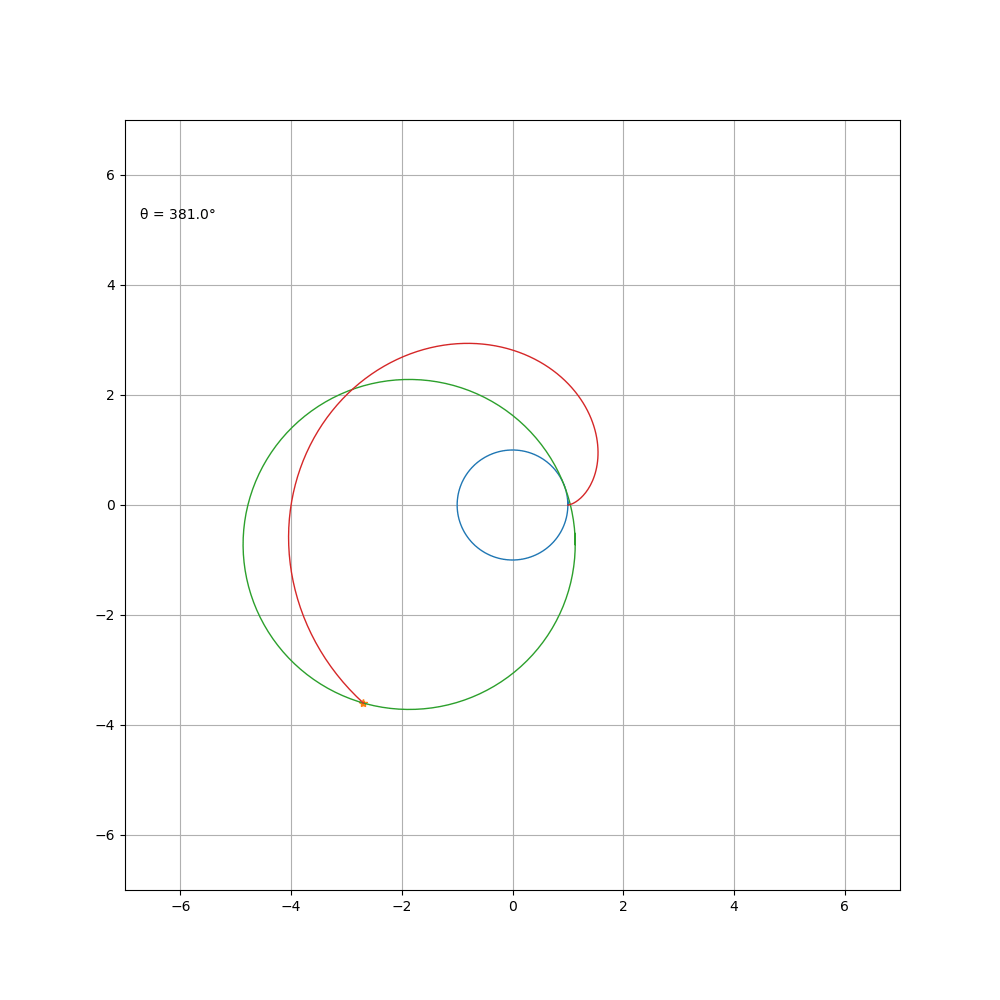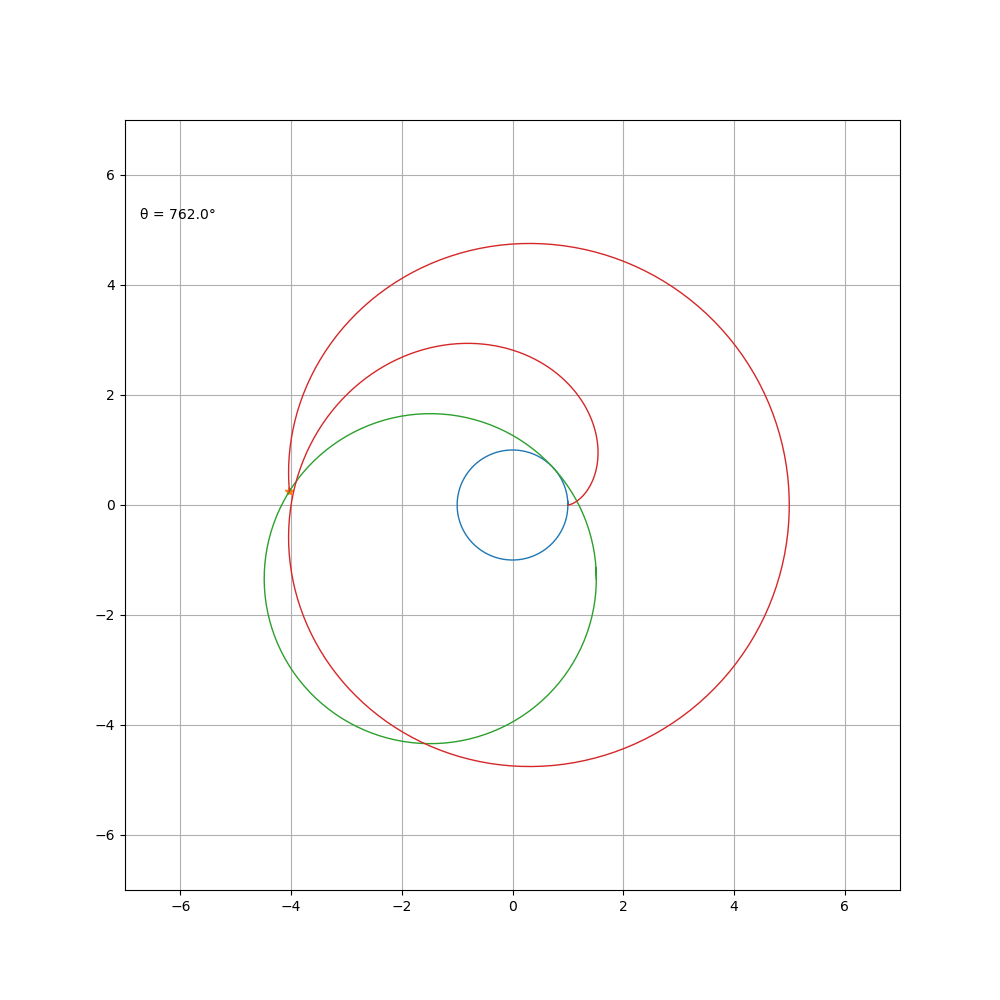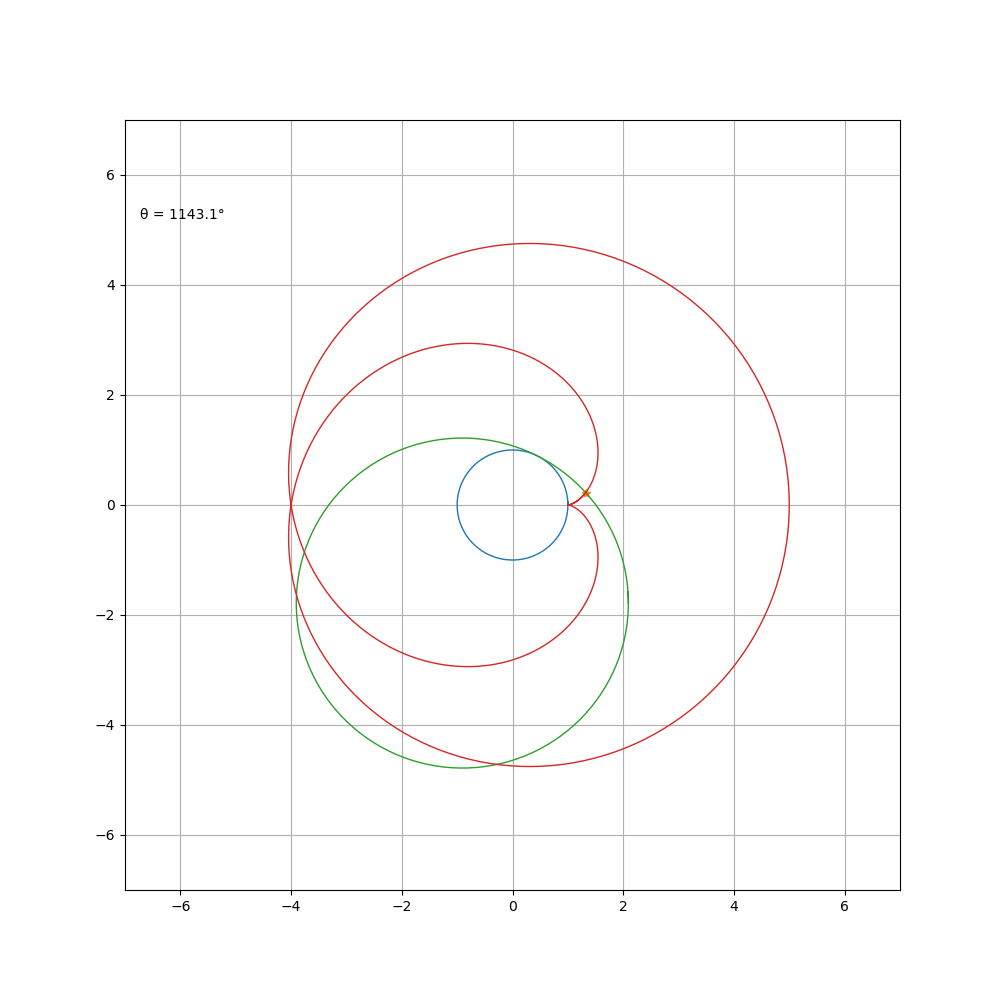
在这里插入图片描述

当 a \b = 4 时，其方程可化简为

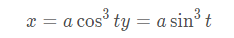
在这里插入图片描述

被称为星形线。

接下来按照惯例，画一下随着 a\ b 比值的变化，内外摆线形状的变化过程

外摆线

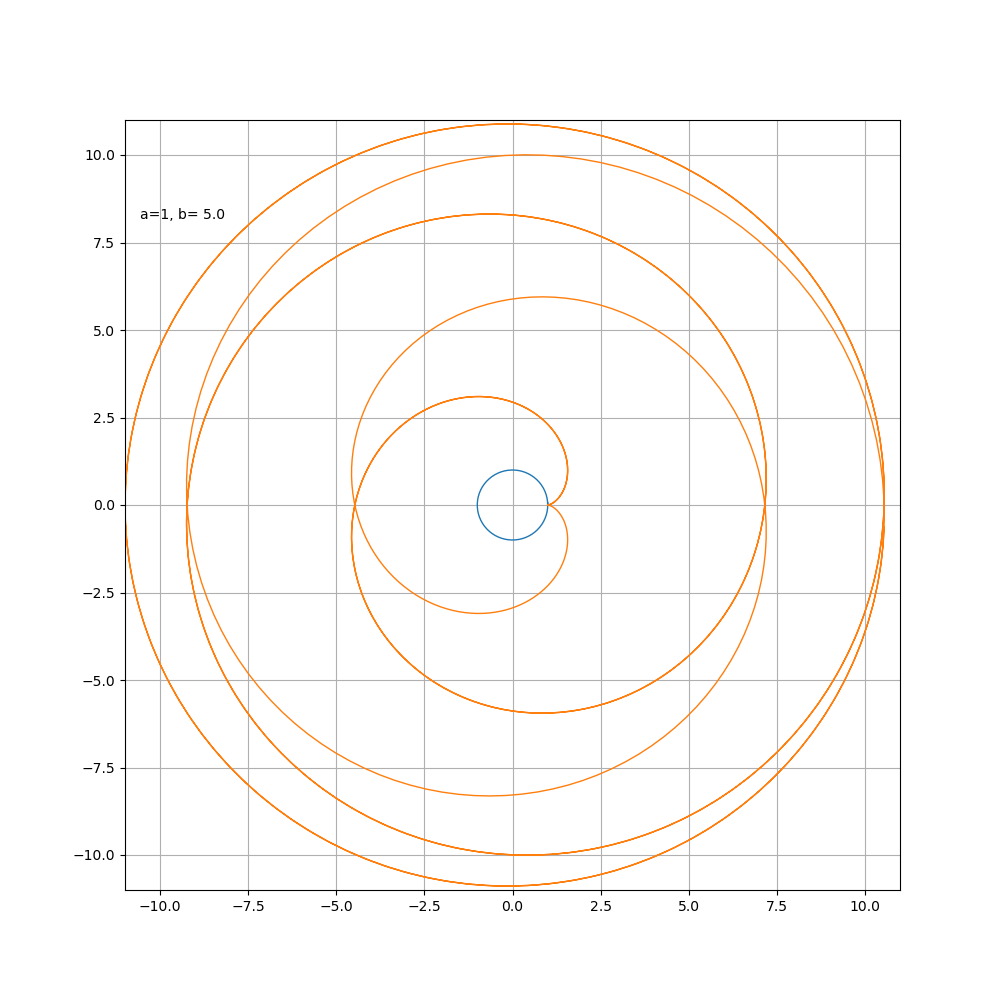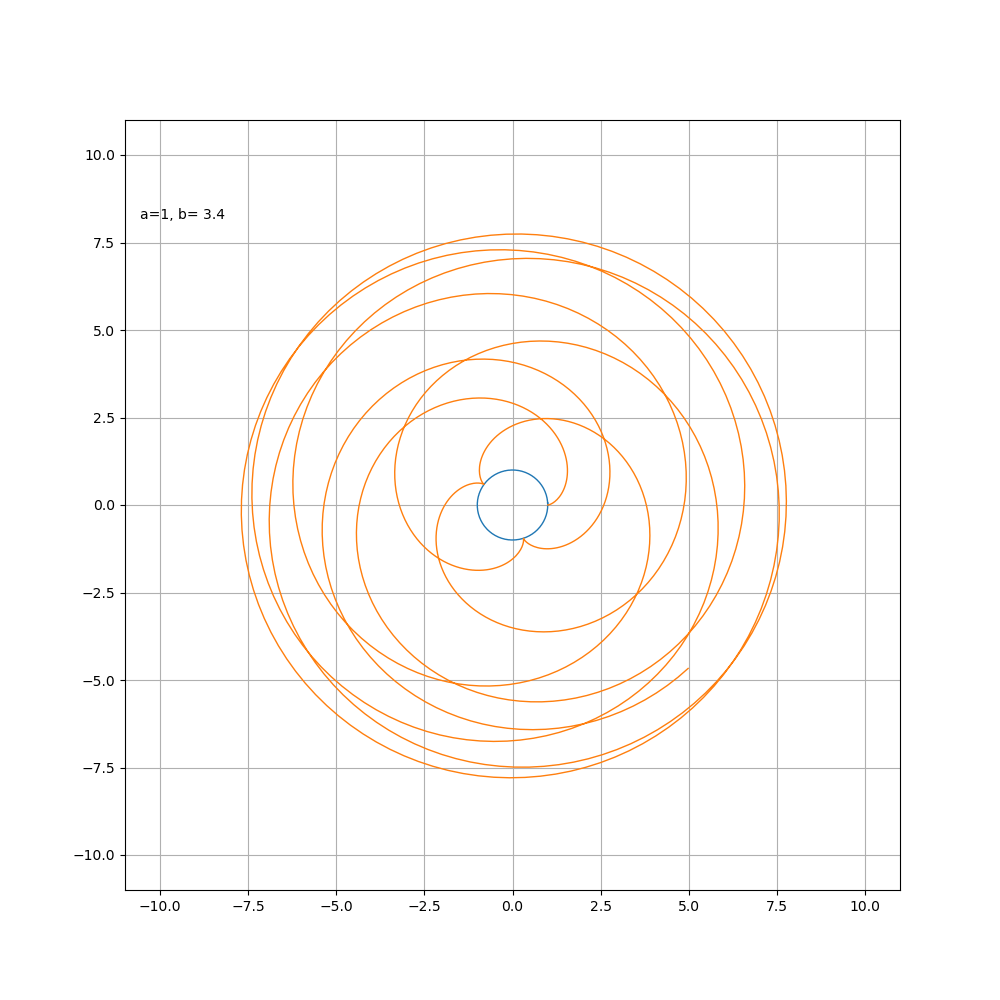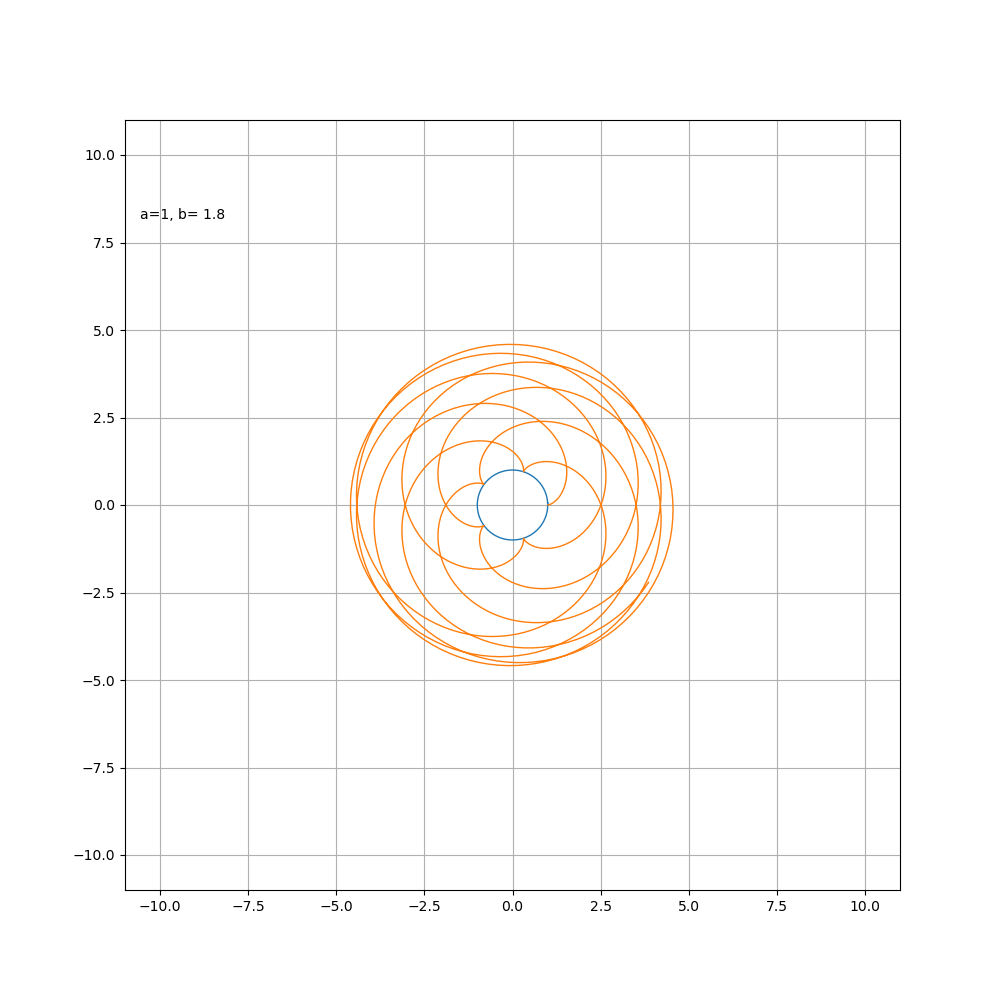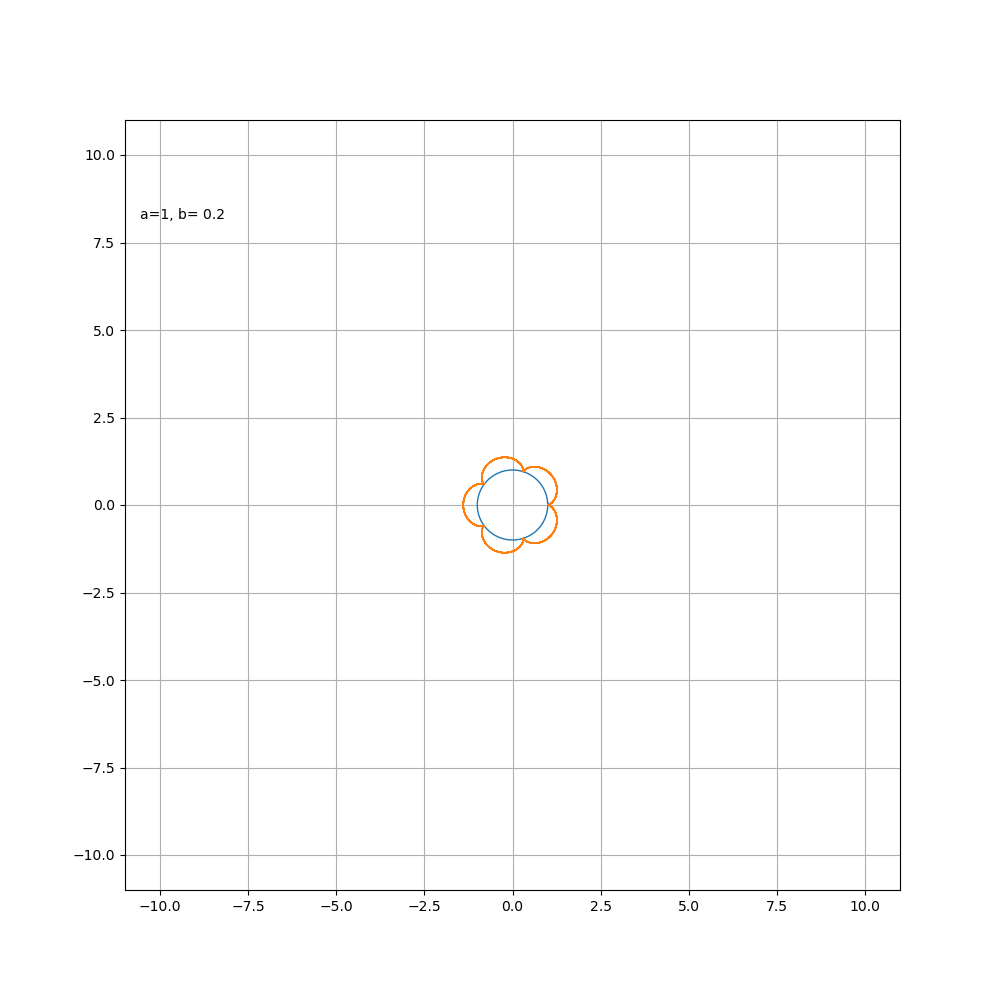
在这里插入图片描述

内摆线

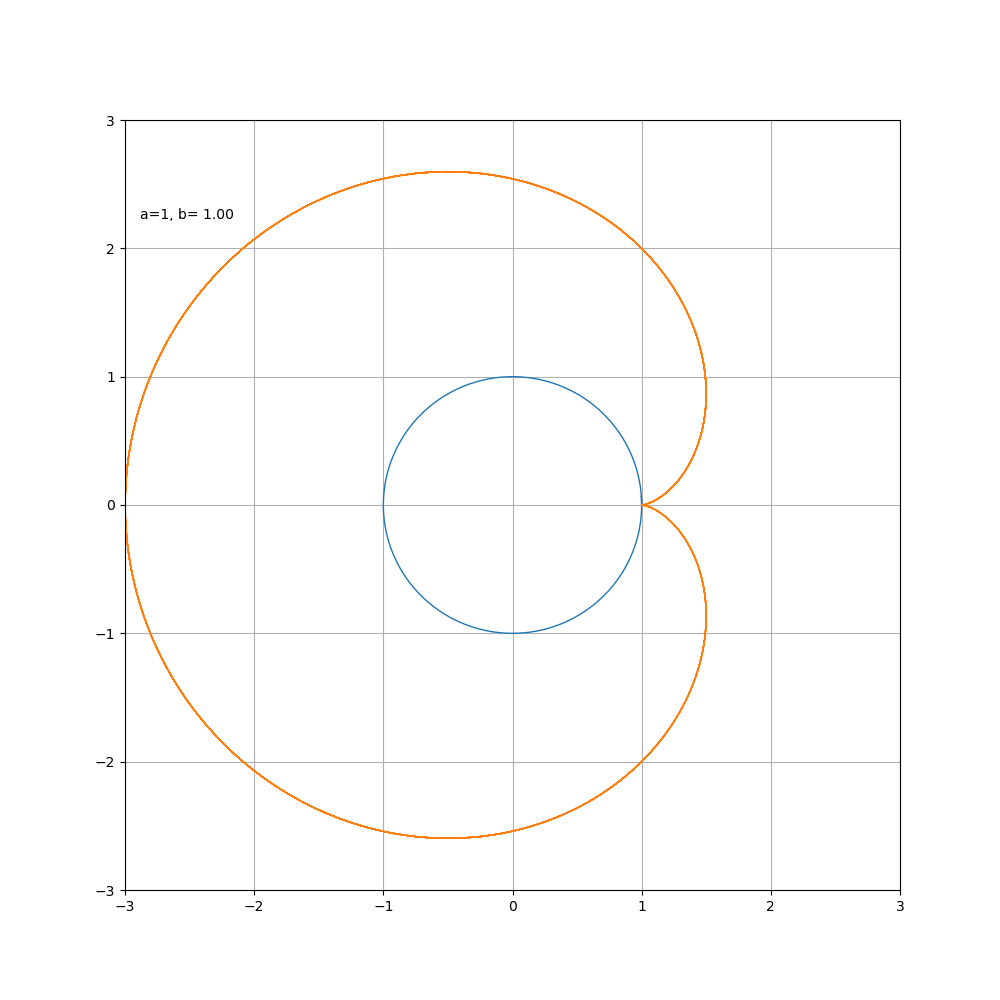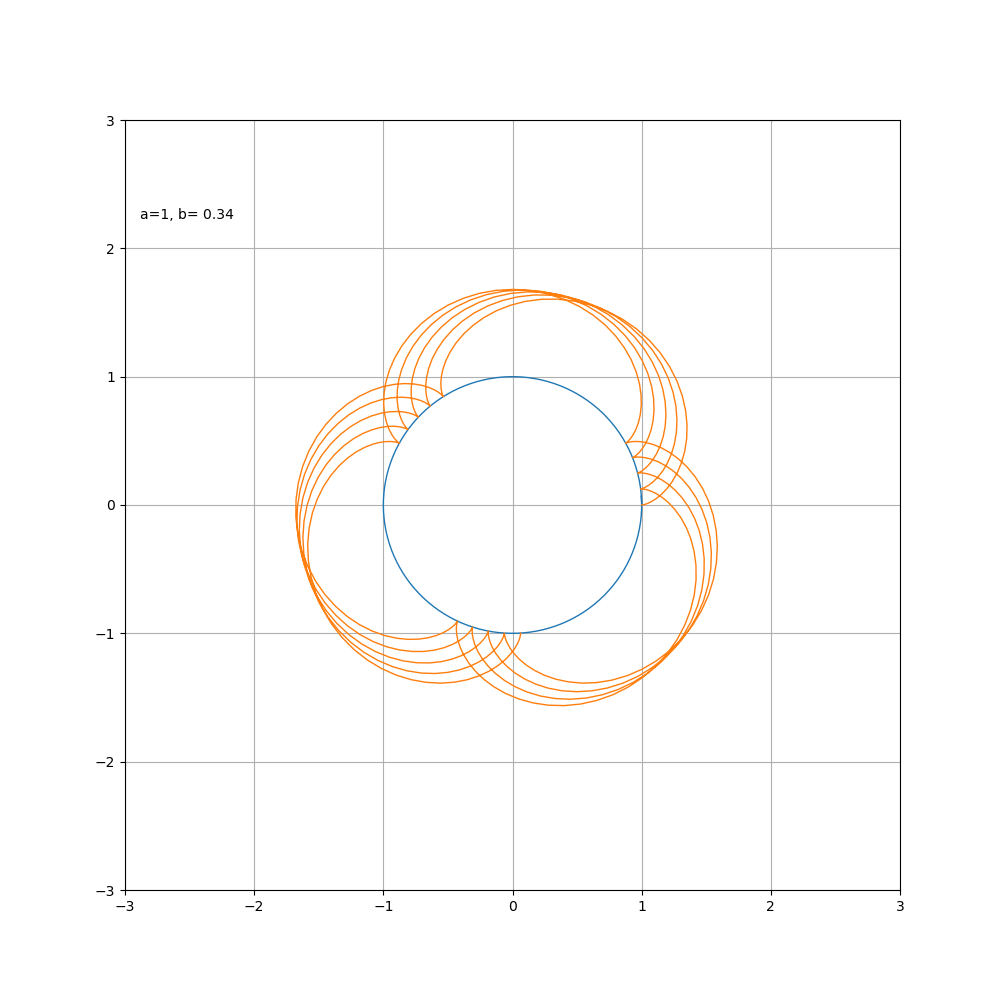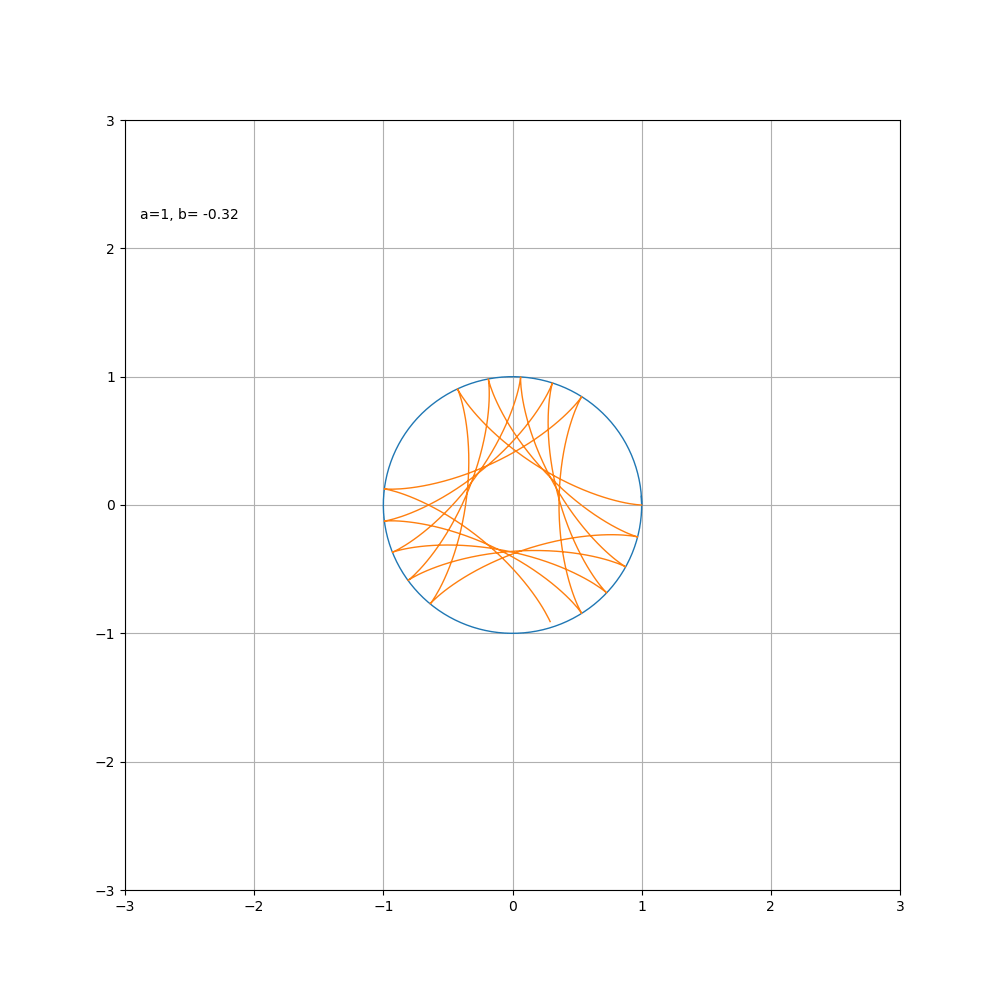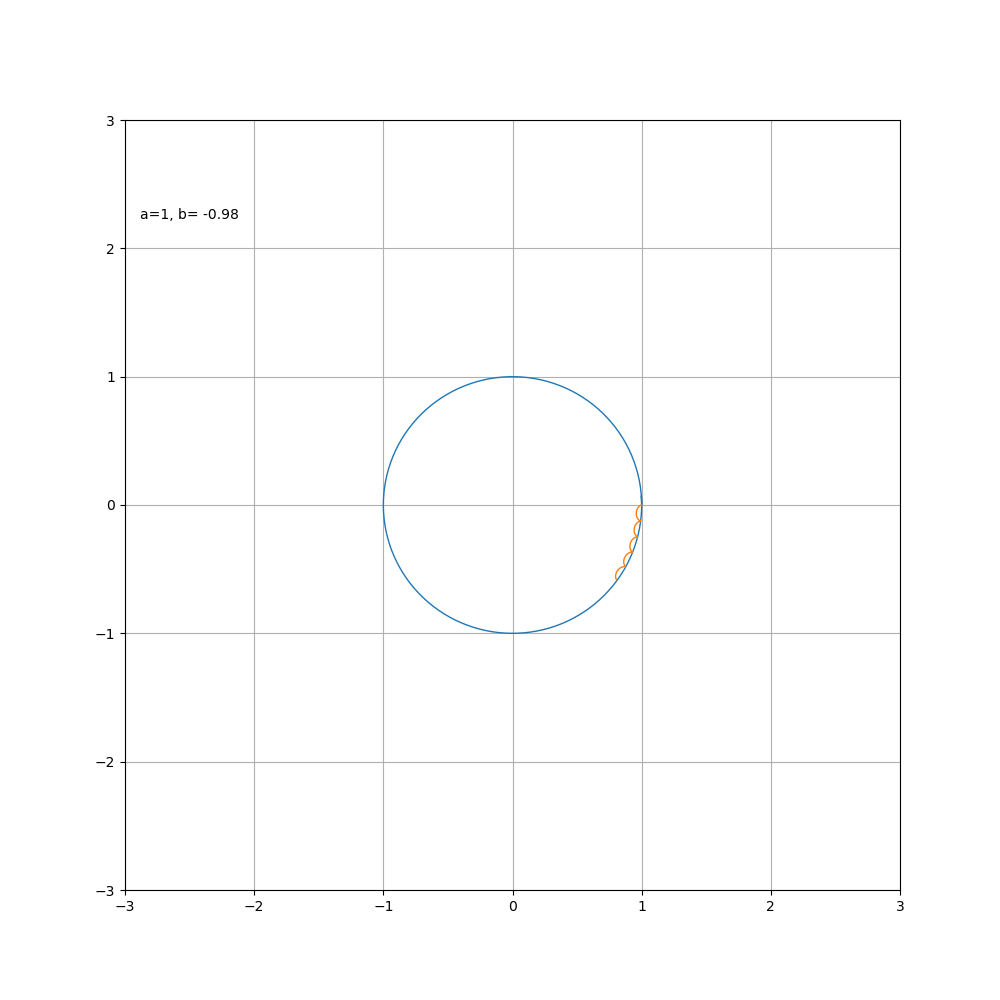
在这里插入图片描述

代码如下

#test.py
import argparse     #用于命令行的交互
parser = argparse.ArgumentParser()
parser.add_argument('bStart', type=float)
parser.add_argument('bEnd', type=float)
args = parser.parse_args()
a = 1
bStart = args.bStart
bEnd = args.bEnd
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(autoscale_on=False, 
    xlim=(-(a+2*bEnd),(a+2*bEnd)),ylim=(-(a+2*bEnd),(a+2*bEnd)))
theta_text = ax.text(0.02,0.85,'',transform=ax.transAxes)
textTemplate = '''a=1, b= %.2f\n'''
ax.grid()
t = np.arange(0,6.4,0.05)
ax.plot(a*np.cos(t),a*np.sin(t),'-',lw=1)
cycloid, = ax.plot([], [], '-', lw=1)
xs,ys = [],[]
t = np.arange(0,30,0.05)
def animate(b):    
    xs = (a+b)*np.cos(t) - b*np.cos((a+b)/b*t)
    ys = (a+b)*np.sin(t) - b*np.sin((a+b)/b*t)
    cycloid.set_data(xs,ys)
    theta_text.set_text(textTemplate % b)
    return cycloid, theta_text
ani = animation.FuncAnimation(fig, animate, np.arange(bEnd,bStart,-0.02), 
    interval=50, blit=True)
plt.show()
ani.save("Cycloid.gif")

在命令行中输入

python test.py -2 2

内摆线和外摆线同常规的摆线一样，皆具有对应的长辐或短辐形式，其标准方程为

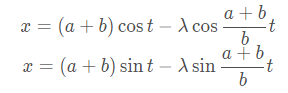
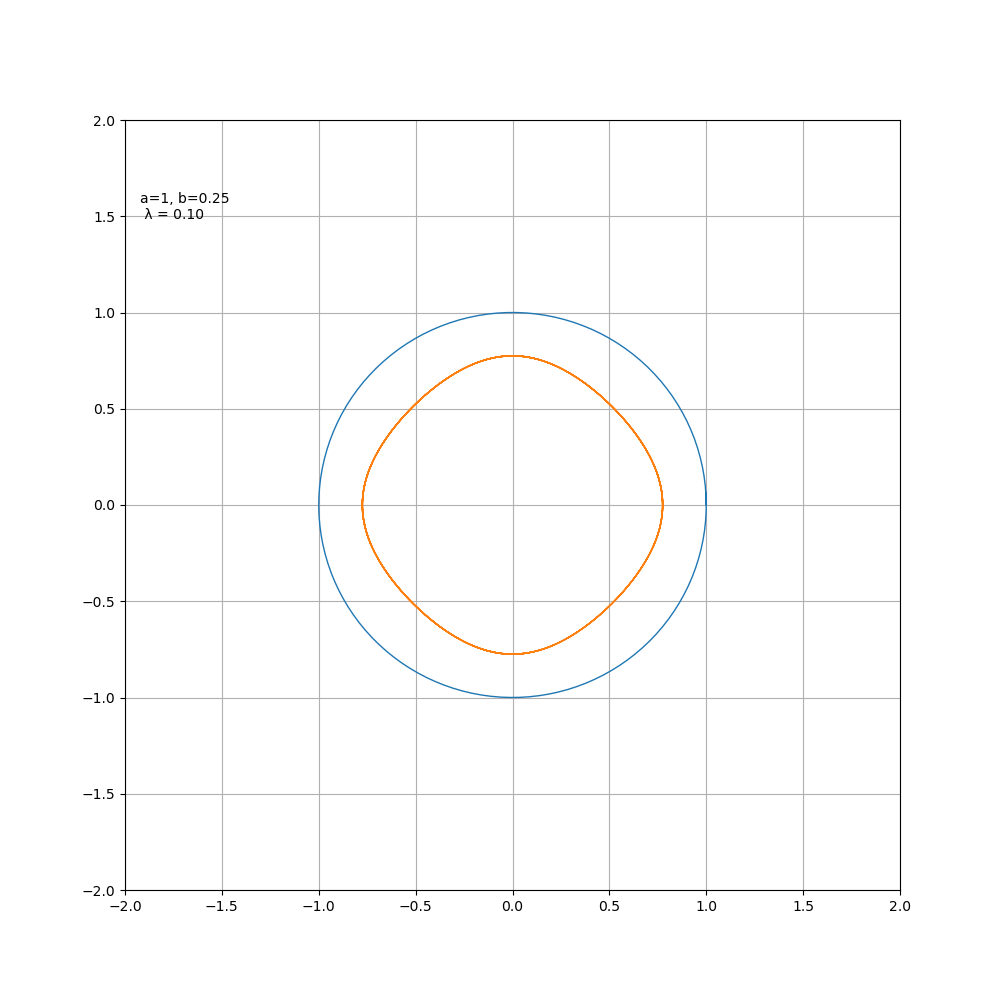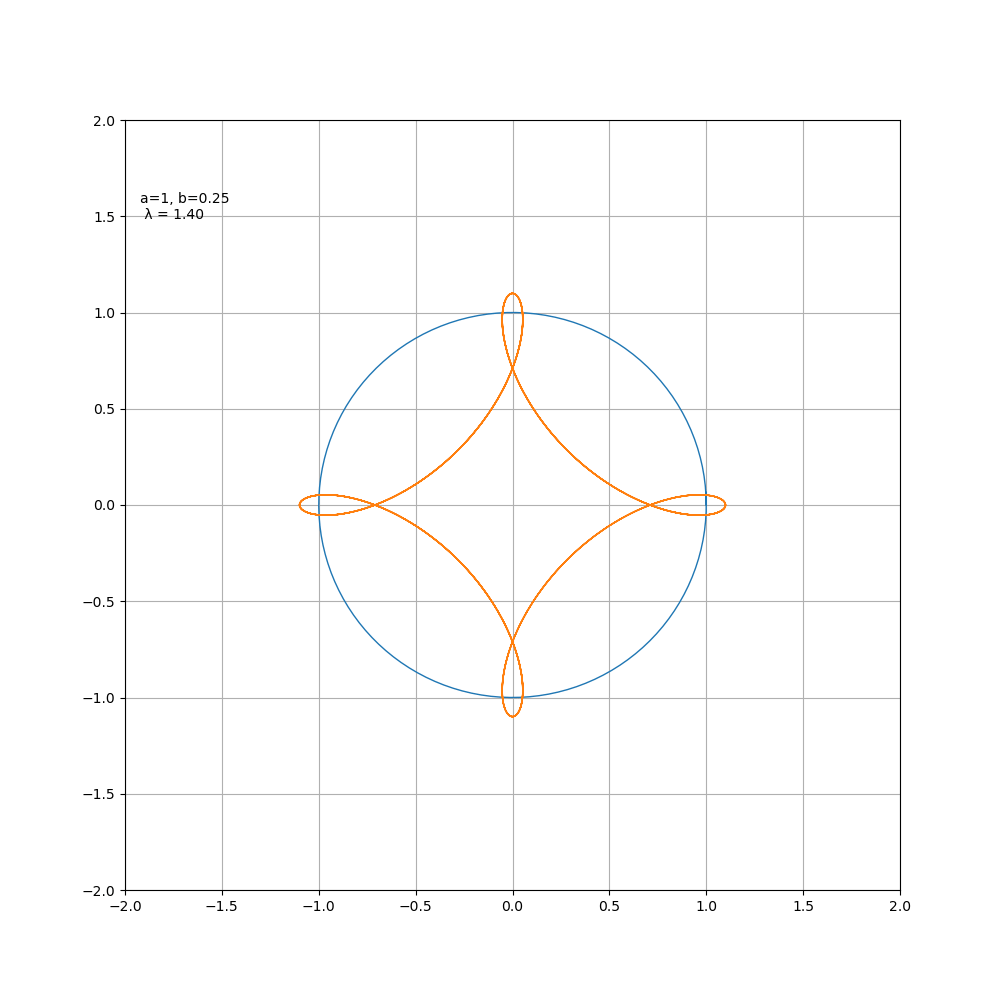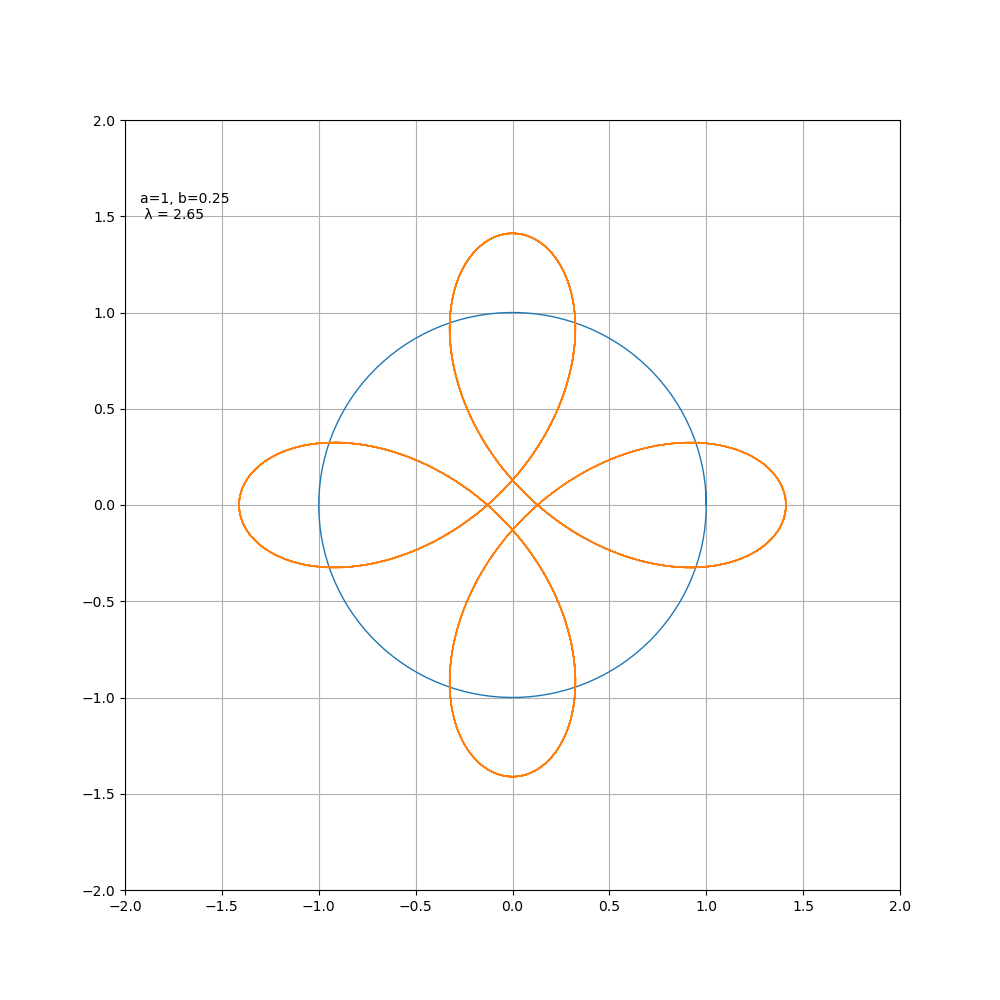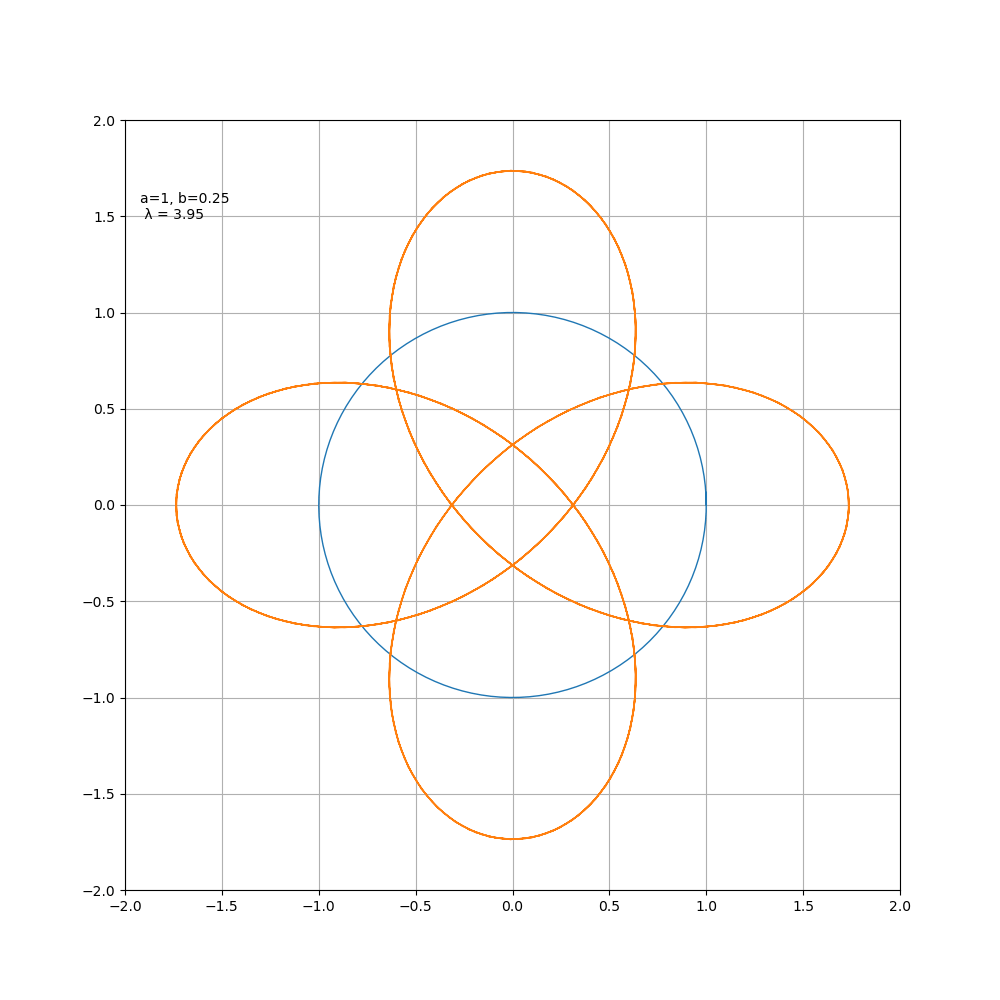
在这里插入图片描述

当 b > 0时为外摆线， b < 0时为内摆线，对于星形线而言，其变化过程如图所示

在这里插入图片描述

以上就是pyhthon绘制超炫酷的心形线星形线摆线的详细内容，更多关于pyhthon绘制心形星形线摆线的资料请关注hwidc其它相关文章！

【文章来源：新加坡服务 欢迎留下您的宝贵建议】
更多阅读