浅析python实现布隆过滤器及Redis中的缓存穿透原理
目录
- 布隆过滤器的原理
- 在 Python 中使用布隆过滤器
- 1、标准布隆过滤器。
- 2、计数布隆过滤器。
- 3、标准扩容布隆过滤器。
- 4、计数扩容布隆过滤器。
- Redis 中使用布隆过滤器
- 最后的话
在开发软件时,我们经常需要判断一个元素是否在一个集合中,比如,如何判断单词的拼写是否错误(判断单词是否在已知的字典中);在网络爬虫里,如何确认一个网址是否已经爬取过;反垃圾邮件系统中,如何判断一个邮件地址是否为垃圾邮件地址等等。
如果这些作为面试题那就很有区分度了,初级工程师就会说,把全部的元素都存在 hash 表中,当需要判断元素是否在集合中时,可以直接判断,时间复杂度是 O(1),比如 Python 的集合:
>>> all_elements = {'a','b','c','d','e'}
>>> 'a' in all_elements
True
>>> 'f' in all_elements
False
>>>
这样回答显然没有考虑到数量级的问题,就拿爬虫中的 URL 去重来说,假设一个 URL 的平均长度是 64 字节,那单纯存储这 10 亿个 URL,需要大约 60GB 的内存空间。因为哈希表必须维持较小的装载因子,才能保证不会出现过多的哈希冲突,导致操作的性能下降。而且,用链表法解决冲突的哈希表,还会存储链表指针,因此哈希表的存储效率一般只有 50%。所以,如果将这 10 亿个 URL 构建成哈希表,那需要的内存空间会超过 100GB。这样的话一般的机器,内存就不够用了,更别提哈希查找了。
因此考虑到这一点,中级一点的工程师会说数据量大的时候可以采用分治的思想,用多台机器(比如 20 台内存是 8GB 的机器)来存储这 10 亿网页链接。这种分治的处理思路,也是一种解决办法,本质上还是增加硬件资源来解决问题,还不够高级。
更高级的工程师会提到位图、布隆过滤器,可以使用很小的内存来实现大数据量的查询。如果你提到了这两个概念,那离 offer 也就不远了。想回答好这个问题,看本文就够了,保证你搞懂布隆过滤器,要是搞不懂,你加我微信,我会对你负责的????。
在讲布隆过滤器前,要先讲一下另一种存储结构,位图(BitMap)。因为,布隆过滤器本身就是基于位图的,是对位图的一种改进。
同样地,为了方便你理解,我们来简化问题,现在有 1 千万个整数,整数的范围在 1 到 1 亿之间。如何快速查找某个整数是否在这 1 千万个整数中呢?
当然,这个问题还是可以用哈希表来解决。不过,我们可以使用一种比较“特殊”的哈希表,那就是位图。我们申请一个大小为 1 亿、数据类型为布尔类型(true 或者 false)的数组。我们将这 1 千万个整数作为数组下标,将对应的数组值设置成 true。比如,整数 5 对应下标为 5 的数组值设置为 true,也就是 array[5]=true 。
当我们查询某个整数 K 是否在这 1 千万个整数中的时候,我们只需要将对应的数组值 array[K]取出来,看是否等于 true。如果等于 true,那说明 1 千万整数中包含这个整数 K;相反,就表示不包含这个整数 K。不过,很多语言中提供的布尔类型,大小是 1 个字节的,并不能节省太多内存空间。实际上,表示 true 和 false 两个值,我们只需要用一个二进制位(bit)就可以了。那如何通过编程语言,来表示一个二进制位呢?
这个用语言很难表达,还是给出代码吧,一码胜千言啊。
这里先给出 Java 的,我觉得 Java 的更容易看懂,再给出 Python 的,你可以对比着代码看下,应该很快就理解了。
public class BitMap { // Java中char类型占16bit,也即是2个字节
private char[] bytes;
private int nbits;
public BitMap(int nbits) {
this.nbits = nbits;
this.bytes = new char[nbits/16+1];
}
public void set(int k) {
if (k > nbits) return;
int byteIndex = k / 16;
int bitIndex = k % 16;
bytes[byteIndex] |= (1 << bitIndex);
}
public boolean get(int k) {
if (k > nbits) return false;
int byteIndex = k / 16;
int bitIndex = k % 16;
return (bytes[byteIndex] & (1 << bitIndex)) != 0;
}
}
Python 的实现:
class BitMap(object):
def __init__(self, max_value):
"""
使用多个整型元素来储存数据,每个元素4个字节(32位)
"""
self._size = int((max_value + 31 - 1) / 31) # 计算需要的字节数,字节数也是数组的大小
self.array = [0 for i in range(self._size)] # 数组的元素都初始化为0,每个元素有32位
@staticmethod
def get_element_index(num):
"""
获取该数即将储存的字节在数组中下标
"""
return num // 31
@staticmethod
def get_bit_index(num):
"""
获取该数在元素中的位下标
"""
return num % 31
def set(self, num):
"""
将该数存在对应的元素的对应位置
"""
element_index = self.get_element_index(num)
bit_index = self.get_bit_index(num)
self.array[element_index] = self.array[element_index] | (1 << bit_index)
def get(self, num):
"""
查找该数是否存在与bitmap中
"""
element_index = self.get_element_index(num)
bit_index = self.get_bit_index(num)
if self.array[element_index] & (1 << bit_index):
return True
return False
从上面位图实现的代码中,你应该可以发现,位图通过数组下标来定位数据,所以,访问效率非常高。而且,每个数字用一个二进制位来表示,在数字范围不大的情况下,所需要的内存空间非常小。
比如刚刚那个例子,如果用哈希表存储这 1 千万的数据,数据是 32 位的整型数,每个整数 4 个字节,那总共至少需要 1 千万 * 4 = 40MB 的存储空间。如果我们通过位图的话,数字范围在 1 到 1 亿之间,只需要 1 亿个二进制位,也就是 12MB 左右的存储空间就够了。
位图就是用一个二进制位的 1 来代表一个元素存在,是不是挺简单的?不过,这里我们有个假设,就是数字所在的范围不是很大。如果数字的范围很大,比如刚刚那个问题,数字范围不是 1 到 1 亿,而是 1 到 10 亿,那位图的大小就需要 10 亿个二进制位,也就是 120MB 的大小,消耗的内存空间,增加了 10 倍,如何不增加内存空间来解决问题呢?请继续往下看。
布隆过滤器的原理
这个时候,布隆过滤器就要出场了。布隆过滤器就是为了解决刚刚这个问题,对位图这种数据结构的一种改进。
布隆过滤器是由伯顿·布隆于 1970 年提出的,为了简化说明布隆过滤器的原理,我们降低数据量级:假如数字范围是从 1 到 100 提升到 200,为了不占用太多内存,我们依然使用 100 个二进制位,如果数据个数超过 100 个,就必然存在哈希冲突,怎么办?
因为我们使用 1 位代表一个元素,因此 100 个二进制位,最多代表 100 个元素,但是假如使用 2 位来代表一个元素呢?那就是组合 C(100,2) = 100*99/2 = 4950 个数,是不是可以代表更多?当然了,你还可以使用 3 位代表一个元素,这样可以代表 161700 个数。
我们以使用 2 位二进制位来代表一个元素为例,设计两个 HASH 函数,bit1 = HASH1(num),bit2 = HASH2(num),存入 num 时就把 bit1 和 bit2 都置为 1;判断时就判断 bit1 和 bit2,当 bit1 和 bit2 都为 1 时,就表示 num 存在集合中。
这样会有个问题:两个数 num1 和 num2 经过两个 HASH 函数之后,结果一样,也就是存在 HASH 冲突,这样就可能误判。
实际上,只要让误判的概率足够低,结果就是可信的。假设哈希函数的个数为 k,二进制的位数为 m,元素个数 n,可以从数学上计算出他们与误判率的关系[1](原麦迪逊威斯康星大学曹培教授提供):
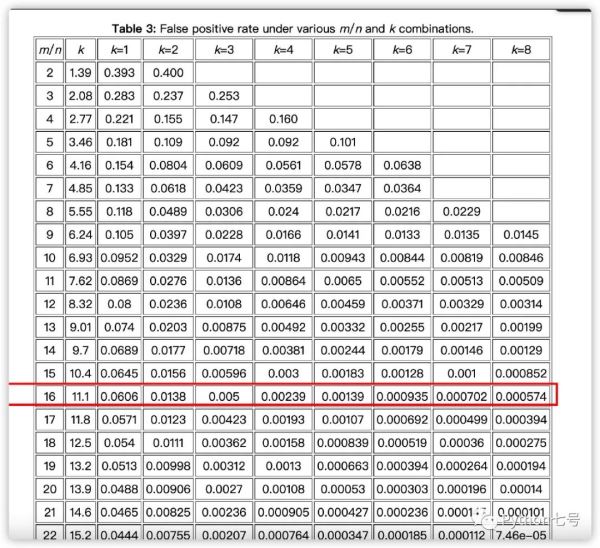
可以看出,当 m/n = 16,n = 8,时,误判率为万分之五,这在大多数应用中都是可以接受的,而且这种误判是这样的:如果这个元素在集合中,那么布隆过滤器绝不会漏掉,如果不在集合中,则有可能判定为在集合中,比如说对应垃圾邮件,布隆过滤器绝不会漏掉黑名单中的任何一个可疑地址,但是它有一定极小的概率将一个不在黑名单上的电子邮件判定为在黑名单中。
到这里我相信你已经明白了个中原理。
在 Python 中使用布隆过滤器
pypi 搜了了 Python 中的布隆过滤器,有 3 个:
pip install bloom-filter2 pip install pybloom-live pip install bloompy
第三个 bloompy[2] 的文档比较详细,推荐使用(如果有兴趣,你可以自己实现一个):
bloompy 提供了四种布隆过滤器:
1、标准布隆过滤器。
标准布隆过滤器只能进行数据的查询和插入,是其他过滤器的基类,可以进行过滤器的存储和恢复,代码示例:
>>> import bloompy
>>> bf = bloompy.BloomFilter(error_rate=0.001,element_num=10**3)
# 查询元素是否在过滤器里返回状态标识
# 如果不在里面则插入,返回False表示元素不在过滤器里
>>> bf.add(1)
False
>>> bf.add(1)
True
>>> 1 in bf
True
>>> bf.exists(1)
True
>>> bf.add([1,2,3])
False
>>> bf.add([1,2,3])
True
>>> [1,2,3] in bf
True
>>> bf.exists([1,2,3])
True
# 将过滤器存储在一个文件里
>>> bf.tofile('filename.suffix')
# 从一个文件里恢复过滤器。自动识别过滤器的种类。
>>> recovered_bf = bloompy.get_filter_fromfile('filename.suffix')
# 或者使用过滤器类的类方法 'fromfile' 来进行过滤器的复原。对应的类只能恢复对应的过滤器
>>> recovered_bf = bloompy.BloomFilter.fromfile('filename.suffix')
# 返回已经插入的元素个数
>>> bf.count
2
# 过滤器的容量
>>> bf.capacity
1000
# 过滤器的位向量
>>> bf.bit_array
bitarray('00....')
# 过滤器位数组长度
>>> bf.bit_num
14400
# 过滤器的哈希种子,默认是素数,可修改
>>> bf.seeds
[2, 3, 5, 7, 11,...]
# 过滤器哈希函数个数
>>> bf.hash_num
10
2、计数布隆过滤器。
它是标准布隆过滤器的子类,但是可以执行删除操作。内置默认使用 4 位二进制位来表示标准布隆过滤器的 1 个位,从而实现可以增减。
>>> import bloompy
>>> cbf = bloompy.CountingBloomFilter(error_rate=0.001,element_num=10**3)
# 与标准布隆过滤器一样
>>> cbf.add(12)
False
>>> cbf.add(12)
True
>>> 12 in cbf
True
>>> cbf.count
1
# 查询元素状态返回标识,如果元素存在过滤器里则删除
>>> cbf.delete(12)
True
>>> cbf.delete(12)
False
>>> 12 in cbf
False
>>> cbf.count
0
# 从文件中恢复过滤器
>>> recovered_cbf = bloompy.CountingBloomFilter.fromfile('filename.suffix')
3、标准扩容布隆过滤器。
当插入的元素个数超过当前过滤器的容量时,自动增加过滤器的容量,默认内置一次扩容 2 倍。支持查询和插入功能。
>>> import bloompy
>>> sbf = bloompy.ScalableBloomFilter(error_rate=0.001,initial_capacity=10**3)
# 默认初次可以设置容量1000
>>> len(sbf)
0
>>> 12 in sbf
False
>>> sbf.add(12)
False
>>> 12 in sbf
True
>>> len(sbf)
1
>>> sbf.filters
[<bloompy.BloomFilter object at 0x000000000B6F5860>]
>>> sbf.capacity
1000
#当过滤器的元素个数达到容量极限时,过滤器会自动增加内置的标准过滤器,
#每次增加2倍容量,自动实现扩容
>>> for i in range(1000):
sbf.add(i)
>>> 600 in sbf
True
>>> len(sbf)
2
>>> sbf.filters
[<bloompy.BloomFilter object at 0x000000000B6F5860>, <bloompy.BloomFilter object at 0x000000000B32F748>]
>>> sbf.capacity
3000
# 从文件中恢复过滤器
>>> recovered_sbf = bloompy.ScalableBloomFilter.fromfile('filename.suffix')
4、计数扩容布隆过滤器。
它是标准扩容布隆过滤器的子类,但支持删除元素的操作。
>>> import bloompy
>>> scbf = bloompy.SCBloomFilter(error_rate=0.001,initial_capacity=10**3)
>>> scbf.add(1)
False
>>> 1 in scbf
True
>>> scbf.delete(1)
True
>>> 1 in scbf
False
>>> len(scbf)
1
>>> scbf.filters
[<bloompy.CountingBloomFilter object at 0x000000000B6F5828>]
# 插入元素使其达到过滤器当前容量极限值
>>> for i in range(1100):
scbf.add(i)
>>> len(scbf)
2
>>> scbf.filters
[<bloompy.CountingBloomFilter object at 0x000000000B6F5828>, <bloompy.CountingBloomFilter object at 0x000000000B6F5898>]
# 从文件中恢复过滤器
>>> recovered_scbf = bloompy.SCBloomFilter.fromfile('filename.suffix')
Redis 中使用布隆过滤器
你可以手动为 Redis 安装 RedisBloom 插件,也可以直接使用官方[3]提供的 docker 版本:
docker run -p 6379:6379 --name redis-redisbloom redislabs/rebloom:latest
然后在 Redis 中就可以这样使用:
127.0.0.1:6379> BF.ADD newFilter foo (integer) 1 127.0.0.1:6379> BF.EXISTS newFilter foo (integer) 1 127.0.0.1:6379> BF.EXISTS newFilter notpresent (integer) 0 127.0.0.1:6379> BF.MADD myFilter foo bar baz 1) (integer) 1 2) (integer) 1 3) (integer) 1 127.0.0.1:6379> BF.MEXISTS myFilter foo nonexist bar 1) (integer) 1 2) (integer) 0 3) (integer) 1
其实 Redis 中使用布隆过滤器还有一个很大的用处,就是处理缓存穿透。Redis 大部分情况都是通过 Key 查询对应的值,假如发送的请求传进来的 key 是不存在 Redis 中的,那么就查不到缓存,查不到缓存就会去数据库查询。假如有大量这样的请求,这些请求像“穿透”了缓存一样直接打在数据库上,这种现象就叫做缓存穿透。
解决方案:
1、把无效的 Key 存进 Redis中。如果 Redis 查不到数据,数据库也查不到,我们把这个 Key 值保存进Redis,设置 value="null",当下次再通过这个 Key 查询时就不需要再查询数据库。这种处理方式肯定是有问题的,假如传进来的这个不存在的 Key 值每次都是随机的,那存进 Redis 也没有意义。
2、使用布隆过滤器。布隆过滤器的作用是某个 key 不存在,那么就一定不存在,它说某个 key 存在,那么很大可能是存在(存在一定的误判率)。于是我们可以在缓存之前再加一层布隆过滤器,在查询的时候先去布隆过滤器查询 key 是否存在,如果不存在就直接返回。
最后的话
布隆过滤器的数学原理在于两个完全随机的数字相冲突的概率很小,因此可以在很小的误判率条件下用很少的空间存储大量的信息,解决误判的常见办法,就是在建立一个小的白名单,存储那些可能被误判的信息。
参考资料
[1]
关系:
http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html
[2]
bloompy:
https://github.com/01ly/bloompy/blob/master/zh-cn.md
[3]
官方:
https://oss.redis.com/redisbloom/Quick_Start/
【文章来源:新加坡服务 欢迎留下您的宝贵建议】