两种java实现二分查找的方式

编辑: admin 分类: java 发布时间: 2021-12-03 来源:互联网

1、二分查找算法思想

有序的序列，每次都是以序列的中间位置的数来与待查找的关键字进行比较，每次缩小一半的查找范围，直到匹配成功。

一个情景：将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

2、二分查找图示说明

图片来源百度图片：

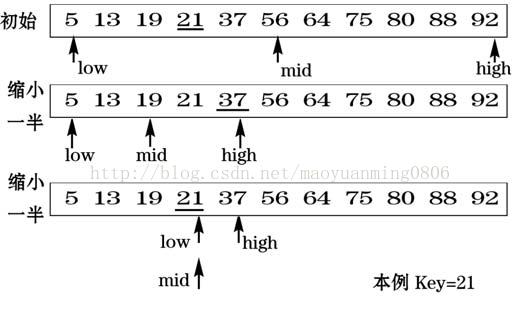
3、二分查找优缺点

优点：

比较次数少，查找速度快，平均性能好；

缺点:

是要求待查表为有序表，且插入删除困难。

因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

使用条件：

查找序列是顺序结构，有序。

3、java代码实现

3.1 使用递归实现

/**
  * 使用递归的二分查找
  *title:recursionBinarySearch
  *@param arr 有序数组
  *@param key 待查找关键字
  *@return 找到的位置
  */
 public static int recursionBinarySearch(int[] arr,int key,int low,int high){
  
  if(key < arr[low] || key > arr[high] || low > high){
   return -1;    
  }
  
  int middle = (low + high) / 2;   //初始中间位置
  if(arr[middle] > key){
   //比关键字大则关键字在左区域
   return recursionBinarySearch(arr, key, low, middle - 1);
  }else if(arr[middle] < key){
   //比关键字小则关键字在右区域
   return recursionBinarySearch(arr, key, middle + 1, high);
  }else {
   return middle;
  } 
  
 }

3.1 不使用递归实现（while循环）

 /**
  * 不使用递归的二分查找
  *title:commonBinarySearch
  *@param arr
  *@param key
  *@return 关键字位置
  */
 public static int commonBinarySearch(int[] arr,int key){
  int low = 0;
  int high = arr.length - 1;
  int middle = 0;   //定义middle
  
  if(key < arr[low] || key > arr[high] || low > high){
   return -1;    
  }
  
  while(low <= high){
   middle = (low + high) / 2;
   if(arr[middle] > key){
    //比关键字大则关键字在左区域
    high = middle - 1;
   }else if(arr[middle] < key){
    //比关键字小则关键字在右区域
    low = middle + 1;
   }else{
    return middle;
   }
  }
  
  return -1;  //最后仍然没有找到，则返回-1
 }

3.3 测试

测试代码：

 public static void main(String[] args) {
 
  int[] arr = {1,3,5,7,9,11};
  int key = 4;
  //int position = recursionBinarySearch(arr,key,0,arr.length - 1);
  
  int position = commonBinarySearch(arr, key);
 
               if(position == -1){
   System.out.println("查找的是"+key+",序列中没有该数！");
  }else{
   System.out.println("查找的是"+key+",找到位置为："+position);
  }
  
 }

recursionBinarySearch()的测试：key分别为0，9，10，15的查找结果

查找的是0,序列中没有该数！

查找的是9,找到位置为：4

查找的是10,序列中没有该数！

查找的是15,序列中没有该数！

commonBinarySearch()的测试：key分别为-1，5，6，20的查找结果

查找的是-1,序列中没有该数！

查找的是5,找到位置为：2

查找的是6,序列中没有该数！

查找的是20,序列中没有该数！

4、时间复杂度

采用的是分治策略

最坏的情况下两种方式时间复杂度一样：O(log2 N)

最好情况下为O（1）

5、空间复杂度

算法的空间复杂度并不是计算实际占用的空间，而是计算整个算法的辅助空间单元的个数

非递归方式：
由于辅助空间是常数级别的所以：空间复杂度是O(1);

递归方式：递归的次数和深度都是log2 N,每次所需要的辅助空间都是常数级别的：

空间复杂度：O(log2N )

到此这篇关于两种java实现二分查找的方式的文章就介绍到这了,更多相关java实现二分查找内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！

【文章由高防cdn提供，感恩】

海外服务器